Таблица умножения

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 умножить на 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл умножения, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее:   4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32

Умножать можно с помощью рук

Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Совет № 3

Знание правил умножения упростит запоминание таблицы умножения:

• При умножении любого числа на 1 получается то число, которое умножали.
• Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
• Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
• Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
• При умножении на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.

Научиться пользоваться таблицей Пифагора

Необходимо показать ребёнку, что числа из левого столбика умножаются на числа из верхней строки. Найти результат очень просто: нужно только провести рукой по таблице вниз и вправо от множителей до места пересечения, где и будет расположен результат умножения.

Возьмите пустую распечатанную или нарисованную таблицу и заполните её вместе с ребёнком. Причем в цвете, закрашивая одинаковый результат одним цветом. Сразу будет видна закономерность. Ребёнок увидит, что запоминать нужно только половину таблицы (согласно переместительному закону умножения).

Понимая смысл умножения, можно использовать для вычислений предыдущие или последующие табличные случаи. При этом случае нужно лишь вычесть или прибавить нужное число.

Другие приемы изучения таблицы умножения

Естественно, единственного верного ответа на вопрос «как правильно учить таблицу умножения» не существует. В каждом отдельном случае, для каждого конкретного ребенка, даже для каждого конкретного урока нужно подбирать определенные наиболее эффективные способы. Попробуйте использовать в своем педагогическом арсенале, несколько приемов работы с вашим ребенком, и тогда вы сможете быстро и легко понять, как лучше научить его таблице умножения. Вот эти способы.

Пример из практики

Выучить любое произведение из таблицы Пифагора будет проще, если продемонстрировать его на практике. Например, у мальчиков можно спросить, сколько всего нужно колес для 5 автомобилей (5×4=20). А таблица умножения для девочек может иметь примеры в стиле, сколько нужно резинок, чтобы заплести по две косички трем куклам (2×3=6).

Сложные примеры

Вашему ребенку какие-то примеры из таблицы умножения могут даваться проще, а какие-то сложнее. Старайтесь тренировать ним именно сложные примеры, чтобы он концентрировался особенно на них.

Таблица умножения на пальцах

Некоторые примеры из таблицы умножения можно легко посчитать, используя пальцы, «природные счеты человека». И это касается не только самых простых произведений, но и, к примеру, умножения на 9. Для этого кладем руки ладонями вниз друг рядом с другом, пальцы нужно выпрямить. Теперь, чтобы умножить любое число на 9 просто загибаем палец под номером этого числа (считая слева). Число пальцев до загнутого будет являться десятками ответа, а после – единицами.

Вообще на пальцах можно считать всю таблицу Пифагора. В данном видео таблицы умножения на пальцах представлены решения более сложных примеров:

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел. Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

iPhones.ru

Превращаем мозг в суперкомпьютер.

Павел Телешевский

У меня 4 новых года: обычный, свой, WWDC и сентябрьская презентация Apple. Последний — самый ожидаемый, и ни капли за это не стыдно.
Instagram/Telegram: @tinelray

Домашнее задание

Для закрепления таблицы умножения на девять мы предлагаем выполнить домашнее задание.

После знака равно поставьте ответ, на выполнение задания дается тридцать секунд.

Задание второе

В этом задании надо ответить на поставленные вопросы быстро и без ошибок.

• сколько будет девятью девять;

• сколько будет девять умножить на шесть;

• сколько получится, если девять умножить на восемь;

• сколько будет девятью три;

• сколько будет девятью пять;

• сколько будет девятью шесть;

• сколько будет, если восемь умножить на девять;

• сколько получится, если четыре умножить на девять;

• сколько будет пятью девять;

• сколько получится, если девять умножить на десять.

Задание третье

В этом задании даны несколько задачек их надо быстро и правильно решить.

Задача 1.

У девяти мальчиков было по шесть шариков. Сколько всего шариков было у детей?

Задача 2.

Девять девочек нарисовали по три рисунка. Сколько всего рисунков нарисовали девочки?

Задача 3.

У каждого енота было по две норки. Енотов я насчитал девять. Сколько всего норок было у енотов?

Задача 4.

К девяти белочкам на праздник сегодня в гости придут столько же разных зверюшек. Сколько всего будет зверей на празднике?

Задача 5.

У Алексея было девять разных игрушек, гости подарили на день рождения Алексею еще столько же игрушек. Сколько игрушек стало у Алексея?

Задача 6.

В музыкальный кружок пришло записываться девять девочек, а мальчиков в три раза больше. Сколько всего детей пришло записываться в музыкальный кружок?

Задание четвертое

Посмотрите следующее задание, здесь даны примеры на умножение, вам надо вместо точек поставить, цифру так, чтобы равенство получилось верным.

Задание пятое

В этом задании даны два столбика, в первом столбике написаны примеры, а во втором написаны ответы.

Надо решить пример правильно, и найти нужный вам ответ, соедините пример и ответ стрелочкой.

Задание шестое

В этом задании даны числа 18, 27, 36, 45, 54, 63, 72, 81, 90.

Какое надо взять число, чтобы получилось следующее равенство?

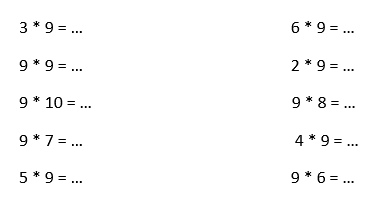
Задание седьмое

В этом задании надо соединить примеры и ответы стрелками.

Смотрите далее:

• Умножение на десять
• Сложение
• Вычитание

Математика для детей разного возраста:

Для лучшего усвоения математического счета и таблицы умножения мы предлагаем вам несколько развивающих игр для детей.

Когда можно приступать к изучению

Согласно Федеральному государственному образовательному стандарту (ФГОС) таблица умножения изучается во втором классе, так как для понимания сути правил умножения ребята должны иметь представление о сложении, ведь умножение — это множественное сложение. Иными словами, чтобы умножить 3 на 4, нужно произвести следующее арифметическое действие: 3+3+3+3. Кроме решения арифметических задач на бумаге, можно использовать игры, например, с игрушками, о которых пойдёт речь ниже. Таким образом, родители, стремящиеся опередить время и изучить с ребёнком таблицу раньше положенного второго класса, должны уяснить, что изучение умножения возможно только тогда, когда малыш понимает принцип сложения.

Для понимания принципа умножения ребёнок должен осознавать суть сложения

С чего начать изучение

На этом этапе лучше воспользоваться классическим вариантом таблицы, а не тем, что обычно печатается на обложках тетрадей. Первым шагом изучения должно стать рассмотрение устройства таблицы, а именно: произведением является число, расположенное на пересечении строки и столбца множителей.

Начиная изучать таблицу, стоит распечатать её в виде плаката и повесить на видном месте в комнате ребёнка

Создаём ситуацию успеха

Таблица со множеством цифр, как правило, сначала вызывает у ребёнка любопытство, но когда дело касается заучивания, приводит в уныние

Поэтому очень важно с самого начала изучения создать ситуацию успеха. А для этого начать с простейших примеров

1. Умножение на 1 — число остаётся «самим собой».
2. Умножаем на 10 — добавляем к числу 0.
3. Умножаем на 2 — складываем два одинаковых числа.
4. Умножение на 0 — всегда равно 0.
5. Перемена множителей — переставляя множители (4х3 или 3х4), произведение будет неизменным. Тут помогает свойство мозга искать во всём симметрию. И здесь же нужно показать юному математику, что достаточно выучить половину каждого ряда таблицы (каждое число, умноженное на 5 включительно), чтобы знать всю.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

2. Умножаем каждый кусочек на второе число.

3. Разбиваем результаты на простые группы одного размера.

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 6000 + 1000 + 40 + 8

27048

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

Умножим число девять на десять

Давайте посмотрим следующий пример, в этом примере десять слагаемых 9, 9, 9, 9, 9, 9, 9, 9, 9, 9. Сложим эти десять слагаемых, что мы получим? Мы получим ответ 90.

9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 90

То есть сумма десяти девяток равна девяносто.

Теперь посмотрим, как можно получить число девяносто путем умножения?

Посмотрите на пример, который написан наверху, у нас в примере десять слагаемых, чтобы получить число девяносто, нам надо цифру девять, умножить на количество слагаемых, то есть на десять получаем девяносто.

9 * 10 = 90

Умножаем девять, на десять получается девяносто.

Девятью десять девяносто

Мы разобрали всю таблицу умножения на девять, теперь посмотрим таблицу умножения на девять всю целиком.

9 * 2 = 18

9 * 3 = 27

9 * 4 = 36

9 * 5 = 45

9 * 6 = 54

9 * 7 = 63

9 * 8 = 72

9 * 9 = 81

9 * 10 = 90

Таблицу умножения на девять можно записать в другом порядке, поменяем множители местами и получим точно такой же ответ.

2 * 9 = 18

3 * 9 = 27

4 * 9 = 36

5 * 9 = 45

6 * 9 = 54

7 * 9 = 63

8 * 9 = 72

9 * 9 = 81

10 * 9 = 90

Чтобы хорошо запомнить таблицу умножения на девять можно поиграть в следующие игры.

Сокращенная таблица умножения до 20

1 x 1 = 11 x 2 = 21 x 3 = 31 x 4 = 41 x 5 = 51 x 6 = 61 x 7 = 71 x 8 = 81 x 9 = 91 x 10 = 10 2 x 1 = 22 x 2 = 42 x 3 = 62 x 4 = 82 x 5 = 102 x 6 = 122 x 7 = 142 x 8 = 162 x 9 = 182 x 10 = 20 3 x 1 = 33 x 2 = 63 x 3 = 93 x 4 = 123 x 5 = 153 x 6 = 183 x 7 = 213 x 8 = 243 x 9 = 273 x 10 = 30 4 x 1 = 44 x 2 = 84 x 3 = 124 x 4 = 164 x 5 = 204 x 6 = 244 x 7 = 284 x 8 = 324 x 9 = 364 x 10 = 40 5 x 1 = 55 x 2 = 105 x 3 = 155 x 4 = 205 x 5 = 255 x 6 = 305 x 7 = 355 x 8 = 405 x 9 = 455 x 10 = 50
6 x 1 = 66 x 2 = 126 x 3 = 186 x 4 = 246 x 5 = 306 x 6 = 366 x 7 = 426 x 8 = 486 x 9 = 546 x 10 = 60 7 x 1 = 77 x 2 = 147 x 3 = 217 x 4 = 287 x 5 = 357 x 6 = 427 x 7 = 497 x 8 = 567 x 9 = 637 x 10 = 70 8 x 1 = 88 x 2 = 168 x 3 = 248 x 4 = 328 x 5 = 408 x 6 = 488 x 7 = 568 x 8 = 648 x 9 = 728 x 10 = 80 9 x 1 = 99 x 2 = 189 x 3 = 279 x 4 = 369 x 5 = 459 x 6 = 549 x 7 = 639 x 8 = 729 x 9 = 819 x 10 = 90 10 x 1 = 1010 x 2 = 2010 x 3 = 3010 x 4 = 4010 x 5 = 5010 x 6 = 6010 x 7 = 7010 x 8 = 8010 x 9 = 9010 x 10 = 100
11 x 1 = 1111 x 2 = 2211 x 3 = 3311 x 4 = 4411 x 5 = 5511 x 6 = 6611 x 7 = 7711 x 8 = 8811 x 9 = 9911 x 10 = 110 12 x 1 = 1212 x 2 = 2412 x 3 = 3612 x 4 = 4812 x 5 = 6012 x 6 = 7212 x 7 = 8412 x 8 = 9612 x 9 = 10812 x 10 = 120 13 x 1 = 1313 x 2 = 2613 x 3 = 3913 x 4 = 5213 x 5 = 6513 x 6 = 7813 x 7 = 9113 x 8 = 10413 x 9 = 11713 x 10 = 130 14 x 1 = 1414 x 2 = 2814 x 3 = 4214 x 4 = 5614 x 5 = 7014 x 6 = 8414 x 7 = 9814 x 8 = 11214 x 9 = 12614 x 10 = 140 15 x 1 = 1515 x 2 = 3015 x 3 = 4515 x 4 = 6015 x 5 = 7515 x 6 = 9015 x 7 = 10515 x 8 = 12015 x 9 = 13515 x 10 = 150
16 x 1 = 1616 x 2 = 3216 x 3 = 4816 x 4 = 6416 x 5 = 8016 x 6 = 9616 x 7 = 11216 x 8 = 12816 x 9 = 14416 x 10 = 160 17 x 1 = 1717 x 2 = 3417 x 3 = 5117 x 4 = 6817 x 5 = 8517 x 6 = 10217 x 7 = 11917 x 8 = 13617 x 9 = 15317 x 10 = 170 18 x 1 = 1818 x 2 = 3618 x 3 = 5418 x 4 = 7218 x 5 = 9018 x 6 = 10818 x 7 = 12618 x 8 = 14418 x 9 = 16218 x 10 = 180 19 x 1 = 1919 x 2 = 3819 x 3 = 5719 x 4 = 7619 x 5 = 9519 x 6 = 11419 x 7 = 13319 x 8 = 15219 x 9 = 17119 x 10 = 190 20 x 1 = 2020 x 2 = 4020 x 3 = 6020 x 4 = 8020 x 5 = 10020 x 6 = 12020 x 7 = 14020 x 8 = 16020 x 9 = 18020 x 10 = 200

Развивающие игры для детей

Игра 1 «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память.

Главная суть игры выбирать цифры, сумма которых равна заданной цифре.

В этой игре дана матрица от одного до шестнадцати. Над матрицей дано число, надо выбрать цифры, сумма которых будет равна заданной цифре.Если вы ответили правильно, вы набираете очки и играете дальше.

Игра 2 «Матрицы памяти»

Игра «Матрицы памяти» развивает память и внимание. Главная суть игры надо воспроизвести положение закрашенных фигур

Главная суть игры надо воспроизвести положение закрашенных фигур.

В каждом раунде показывается игровое поле, состоящее из ячеек, определенное число ячеек закрашено, остальное остается свободное. Надо запомнить расположение этих ячеек и повторить их положение после того как, они исчезли на экране. Если вы правильно отмечаете ячейки, вы набираете баллы и переходите дальше.

Умножим число девять на четыре

Давайте посмотрим следующий пример, в этом примере четыре слагаемых 9, 9, 9, 9. Сложим эти четыре слагаемых, что мы получим? Мы получим ответ 36.

9 + 9 + 9 + 9 = 36

То есть сумма четырех девяток равна тридцати шести.

Теперь посмотрим, как можно получить число тридцать шесть путем умножения?

Посмотрите на пример, который написан наверху, у нас в примере четыре слагаемых, чтобы получить число тридцать шесть, нам надо цифру девять, умножить на количество слагаемых, то есть на четыре получаем тридцать шесть.

9* 4 = 36

Умножаем девять, на четыре получается тридцать шесть.

Девятью четыре тридцать шесть

Вы здесь

Главная » Еще

Без ответов

Таблица умножения без ответов.

Вариант 2

Таблица деления без ответов.

Чтобы скачать и распечатать таблицу умножения и деления без ответов, нужно нажать правую кнопку мышки и выбрать «сохранить картинку как».

Файлы: 

Вложение	Размер
Таблица умножения без ответов	8.75 КБ
Таблица деления без ответов	9.1 КБ

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Таблица умножения с помощью пальцев на 6, 7 и 8: схемы с подробным описанием

Подготовим правильное положение рук

Первым делом нужно, чтобы руки ребенка приняли правильную позицию. Для этого поставим их перед собой, развернув ладонями к лицу. При этом старайтесь немного их направить в сторону друг друга, поскольку работать нужно будет по методу касания пальцев. То есть, мизинцы должны находиться внизу. На каждой руке пальцы будут обозначать одни и те же цифры:

Большой палец, как задорный толстяк,

Пусть носит звание – 10-й добряк!

Указательный, да господин влиятельный

Солнечной 9-ой опознавательный.

Средний палец – хулиган

В бесконечную 8-ку зван!

Безымянный, который окольцованный,

Еще и магической 7-ой заколдованный!

Наш любимец – малой мизинец

Получил 6-ой гостинец!

Таким образом, мы подготовились к умножению на пальцах. Далее выбираем пример, который хотим решить.

Дайте пальцам не только счет, но и прозвища

Рассмотрим пример таблицы умножения 6 на 7

• Цифру 6 на левой руке у нас означает мизинец, а цифру 7 – безымянный палец, но на правой руке.
• Нам нужно соединить их вместе, соприкасаясь стыками подушечек. При таком соприкосновении другие пальцы остаются свободными.

Дабы усвоить материал, предлагаем вернуться к нашему примеру:

1. На левой руке у нас только один палец, что с шестым гостинцем. Он у нас в соединении.
2. На правой руке уже два пальца – мизинец, что внизу конструкции, и безымянный, который в стыке с левой рукой.

Умножение 6 на 7

• Таким образом, в числе нашего результата в разряде десятков будет стоять цифра 3. То есть, три пальца означают 30. На фото имеют голубой цвет. 
• А чтобы узнать цифру разряда единиц, нужно сосчитать по отдельности оставшиеся свободные пальцы на обеих руках и перемножить их между собой. Они пронумерованы синим цветом на верхнем фото.
• В нашем случае:
  • На левой руке остались свободными 4 пальца – толстяк, господин, хулиган и безымянный
  • На правой руке остались свободными 3 пальца – средний и указательный, а также большой
• Нам нужно 3 умножить на 4. Таким образом, мы получили цифру разряда единиц – это 12.
• В завершение к 30 добавляем наши 12-е единицы и получаем 42!

Может быть вариант еще намного проще, когда при умножении верхних свободных пальцев для получения цифры разряда единиц результат получается меньше 9. В таком случае сложить вместе два числа куда проще даже первоклассникам.

Если ваш малыш еще не до автоматизма усвоил материал, тогда разбейте суммирование на этапы:

• 3 – это десятки
• Число 12 – это 1 десяток и 2 единицы
• В итоге мы складываем 3+1, получаем 4 десятка
• А к ним уже добавляем оставшиеся 2 единицы
• И получаем 42
• Результатом умножения 6 на 7 или 7 на 6, поскольку разницы никакой нет, будет число 42.

Небольшая проверка на внимательность

Рассмотрим пример таблицы умножения 7 на 10

Несмотря на простоту такого умножения, у детворы порой возникают трудности с пониманием самой схемы. Поэтому такой простой пример стоит рассматривать после базового разбора пальцевой методики. Нумеровать пальцы нужно точно в такой же последовательности:

• цифру 7 означает безымянный палец левой руки
• а цифру 10 – большой толстяк

И теперь мы состыковываем большой палец с безымянным.

Умножение 7 на 10

• Таким образом, для получения цифры разряда десятков нужно прибавить к двум пальцам левой руки все пять фаланг правой. В итоге мы получаем цифру 7. То есть, 70.
• Для получения цифры разряда единиц нужно 4 свободных пальца левой руки умножить на 0 свободных пальцев правой руки. В результате получаем 0.
• В итоге к 70 мы добавляем 0, но получаем те же 70. Перепроверяем результат!

Таблица умножения на 8: пример 8 на 8

1. Состыковываем наши средние пальцы, поскольку они отвечают за цифру 8.

Умножаем 8 на 8

1. Внизу у нас по 2 пальца на каждой руке и еще 2 в замке. В итоге мы имеем 6 пальцев. То есть, 60.
2. Вверху конструкции осталось 4 свободных пальца. То есть, мы умножаем 2 на 2 и получаем 4. Достаточно просто, ведь их можно и сложить, и умножить, а получить один и тот же результат.
3. В итоге к 6 десяткам мы добавляем 4 и получаем 64!

Классическая таблица умножения до 20

1 x 1 = 11 x 2 = 21 x 3 = 31 x 4 = 41 x 5 = 51 x 6 = 61 x 7 = 71 x 8 = 81 x 9 = 91 x 10 = 101 x 11 = 111 x 12 = 121 x 13 = 131 x 14 = 141 x 15 = 151 x 16 = 161 x 17 = 171 x 18 = 181 x 19 = 191 x 20 = 20 2 x 1 = 22 x 2 = 42 x 3 = 62 x 4 = 82 x 5 = 102 x 6 = 122 x 7 = 142 x 8 = 162 x 9 = 182 x 10 = 202 x 11 = 222 x 12 = 242 x 13 = 262 x 14 = 282 x 15 = 302 x 16 = 322 x 17 = 342 x 18 = 362 x 19 = 382 x 20 = 40 3 x 1 = 33 x 2 = 63 x 3 = 93 x 4 = 123 x 5 = 153 x 6 = 183 x 7 = 213 x 8 = 243 x 9 = 273 x 10 = 303 x 11 = 333 x 12 = 363 x 13 = 393 x 14 = 423 x 15 = 453 x 16 = 483 x 17 = 513 x 18 = 543 x 19 = 573 x 20 = 60 4 x 1 = 44 x 2 = 84 x 3 = 124 x 4 = 164 x 5 = 204 x 6 = 244 x 7 = 284 x 8 = 324 x 9 = 364 x 10 = 404 x 11 = 444 x 12 = 484 x 13 = 524 x 14 = 564 x 15 = 604 x 16 = 644 x 17 = 684 x 18 = 724 x 19 = 764 x 20 = 80 5 x 1 = 55 x 2 = 105 x 3 = 155 x 4 = 205 x 5 = 255 x 6 = 305 x 7 = 355 x 8 = 405 x 9 = 455 x 10 = 505 x 11 = 555 x 12 = 605 x 13 = 655 x 14 = 705 x 15 = 755 x 16 = 805 x 17 = 855 x 18 = 905 x 19 = 955 x 20 = 100
6 x 1 = 66 x 2 = 126 x 3 = 186 x 4 = 246 x 5 = 306 x 6 = 366 x 7 = 426 x 8 = 486 x 9 = 546 x 10 = 606 x 11 = 666 x 12 = 726 x 13 = 786 x 14 = 846 x 15 = 906 x 16 = 966 x 17 = 1026 x 18 = 1086 x 19 = 1146 x 20 = 120 7 x 1 = 77 x 2 = 147 x 3 = 217 x 4 = 287 x 5 = 357 x 6 = 427 x 7 = 497 x 8 = 567 x 9 = 637 x 10 = 707 x 11 = 777 x 12 = 847 x 13 = 917 x 14 = 987 x 15 = 1057 x 16 = 1127 x 17 = 1197 x 18 = 1267 x 19 = 1337 x 20 = 140 8 x 1 = 88 x 2 = 168 x 3 = 248 x 4 = 328 x 5 = 408 x 6 = 488 x 7 = 568 x 8 = 648 x 9 = 728 x 10 = 808 x 11 = 888 x 12 = 968 x 13 = 1048 x 14 = 1128 x 15 = 1208 x 16 = 1288 x 17 = 1368 x 18 = 1448 x 19 = 1528 x 20 = 160 9 x 1 = 99 x 2 = 189 x 3 = 279 x 4 = 369 x 5 = 459 x 6 = 549 x 7 = 639 x 8 = 729 x 9 = 819 x 10 = 909 x 11 = 999 x 12 = 1089 x 13 = 1179 x 14 = 1269 x 15 = 1359 x 16 = 1449 x 17 = 1539 x 18 = 1629 x 19 = 1719 x 20 = 180 10 x 1 = 1010 x 2 = 2010 x 3 = 3010 x 4 = 4010 x 5 = 5010 x 6 = 6010 x 7 = 7010 x 8 = 8010 x 9 = 9010 x 10 = 10010 x 11 = 11010 x 12 = 12010 x 13 = 13010 x 14 = 14010 x 15 = 15010 x 16 = 16010 x 17 = 17010 x 18 = 18010 x 19 = 19010 x 20 = 200
11 x 1 = 1111 x 2 = 2211 x 3 = 3311 x 4 = 4411 x 5 = 5511 x 6 = 6611 x 7 = 7711 x 8 = 8811 x 9 = 9911 x 10 = 11011 x 11 = 12111 x 12 = 13211 x 13 = 14311 x 14 = 15411 x 15 = 16511 x 16 = 17611 x 17 = 18711 x 18 = 19811 x 19 = 20911 x 20 = 220 12 x 1 = 1212 x 2 = 2412 x 3 = 3612 x 4 = 4812 x 5 = 6012 x 6 = 7212 x 7 = 8412 x 8 = 9612 x 9 = 10812 x 10 = 12012 x 11 = 13212 x 12 = 14412 x 13 = 15612 x 14 = 16812 x 15 = 18012 x 16 = 19212 x 17 = 20412 x 18 = 21612 x 19 = 22812 x 20 = 240 13 x 1 = 1313 x 2 = 2613 x 3 = 3913 x 4 = 5213 x 5 = 6513 x 6 = 7813 x 7 = 9113 x 8 = 10413 x 9 = 11713 x 10 = 13013 x 11 = 14313 x 12 = 15613 x 13 = 16913 x 14 = 18213 x 15 = 19513 x 16 = 20813 x 17 = 22113 x 18 = 23413 x 19 = 24713 x 20 = 260 14 x 1 = 1414 x 2 = 2814 x 3 = 4214 x 4 = 5614 x 5 = 7014 x 6 = 8414 x 7 = 9814 x 8 = 11214 x 9 = 12614 x 10 = 14014 x 11 = 15414 x 12 = 16814 x 13 = 18214 x 14 = 19614 x 15 = 21014 x 16 = 22414 x 17 = 23814 x 18 = 25214 x 19 = 26614 x 20 = 280 15 x 1 = 1515 x 2 = 3015 x 3 = 4515 x 4 = 6015 x 5 = 7515 x 6 = 9015 x 7 = 10515 x 8 = 12015 x 9 = 13515 x 10 = 15015 x 11 = 16515 x 12 = 18015 x 13 = 19515 x 14 = 21015 x 15 = 22515 x 16 = 24015 x 17 = 25515 x 18 = 27015 x 19 = 28515 x 20 = 300
16 x 1 = 1616 x 2 = 3216 x 3 = 4816 x 4 = 6416 x 5 = 8016 x 6 = 9616 x 7 = 11216 x 8 = 12816 x 9 = 14416 x 10 = 16016 x 11 = 17616 x 12 = 19216 x 13 = 20816 x 14 = 22416 x 15 = 24016 x 16 = 25616 x 17 = 27216 x 18 = 28816 x 19 = 30416 x 20 = 320 17 x 1 = 1717 x 2 = 3417 x 3 = 5117 x 4 = 6817 x 5 = 8517 x 6 = 10217 x 7 = 11917 x 8 = 13617 x 9 = 15317 x 10 = 17017 x 11 = 18717 x 12 = 20417 x 13 = 22117 x 14 = 23817 x 15 = 25517 x 16 = 27217 x 17 = 28917 x 18 = 30617 x 19 = 32317 x 20 = 340 18 x 1 = 1818 x 2 = 3618 x 3 = 5418 x 4 = 7218 x 5 = 9018 x 6 = 10818 x 7 = 12618 x 8 = 14418 x 9 = 16218 x 10 = 18018 x 11 = 19818 x 12 = 21618 x 13 = 23418 x 14 = 25218 x 15 = 27018 x 16 = 28818 x 17 = 30618 x 18 = 32418 x 19 = 34218 x 20 = 360 19 x 1 = 1919 x 2 = 3819 x 3 = 5719 x 4 = 7619 x 5 = 9519 x 6 = 11419 x 7 = 13319 x 8 = 15219 x 9 = 17119 x 10 = 19019 x 11 = 20919 x 12 = 22819 x 13 = 24719 x 14 = 26619 x 15 = 28519 x 16 = 30419 x 17 = 32319 x 18 = 34219 x 19 = 36119 x 20 = 380 20 x 1 = 2020 x 2 = 4020 x 3 = 6020 x 4 = 8020 x 5 = 10020 x 6 = 12020 x 7 = 14020 x 8 = 16020 x 9 = 18020 x 10 = 20020 x 11 = 22020 x 12 = 24020 x 13 = 26020 x 14 = 28020 x 15 = 30020 x 16 = 32020 x 17 = 34020 x 18 = 36020 x 19 = 38020 x 20 = 400

По запросам в Интернете часто предлагают сокращенный вариант таблицы до 20, в котором отсутствует часть самых сложных примеров.

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»