Примеры по математике 3 класс

Составные задачи на нахождение суммы

1. В читальном зале 12 стеллажей книг со сказками, а с рассказами о животных в 3 раза меньше. Сколько всего стеллажей с книгами сказок и рассказов о животных в читальном зале?2. В кабинете музыки 5 трещоток, а бубнов в 2 раза больше. Сколько всего музыкальных инструментов в кабинете музыки?3. Тётя Тамара посадила на участке 10 кустов красной земляники, а кустов жёлтой земляники в 2 раза меньше. Сколько всего кустов земляники посадила тётя Тамара?4. На выставке кошек владельцы показывали 22 сиамские кошки, а персидских кошек в 2 раза меньше, чем сиамских. Сколько всего кошек показывали владельцы на выставке?5. В олимпиаде по математике участвовало 12 мальчиков, а девочек в 4 раза меньше, чем мальчиков. Сколько всего детей участвовало в олимпиаде по математике?6. На экскурсию по Москве в автобусе ехало 36 учеников, а в легковой автомашине в 9 раз меньше, чем в автобусе. Сколько всего учеников ехало на экскурсию?7. В корзине 5 красных яблок, а жёлтых яблок в 3 раза больше, чем красных. Сколько всего яблок в корзине?8. В мастерской ремонтировали 48 цветных телевизоров, а чёрно-белых в 6 раз меньше, чем цветных. Сколько всего телевизоров ремонтировали в мастерской?9. В портфеле лежало 2 учебника, а тетрадей в 2 раза больше, чем учебников. Сколько учебников и тетрадей лежало в портфеле?10. Для украшения класса взяли 4 гирлянды с жёлтыми лампочками, а с зелёными лампочками в 2 раза больше, чем с жёлтыми. Сколько всего гирлянд взяли для украшения класса?

(косвенная форма)

1. В городе 100 зоомагазинов. Это в 4 раза меньше, чем супермаркетов. Сколько всего зоомагазинов и супермаркетов в городе?2. В секции плавания занимаются 45 мальчиков. Это в 5 раз больше, чем девочек. Сколько девочек и мальчиков занимаются плаванием?3. Продали 9 кг фундука. Это в 5 раз меньше, чем грецких орехов. Сколько всего килограммов фундука и грецких орехов продали?4. Из абрикосов сделали 27 кг урюка. Это в 3 раза больше, чем кураги. Сколько всего килограммов урюка и кураги сделали из абрикосов?5. К празднику купили 36 красных воздушных шариков. Это в 4 раза больше, чем синих. Сколько всего воздушных шариков купили к празднику?6. Утром срезали 12 гладиолусов. Это в 3 раза меньше, чем срезали вечером. Сколько всего гладиолусов срезали утром и вечером?7. В столовом сервизе 12 тарелок. Это в 2 раза больше, чем в чайном. Сколько тарелок в чайном и столовом сервизах вместе?8. На автобазе было 48 грузовых машин, что в 6 раз больше, чем легковых. Сколько всего машин на автобазе?9. В ёлочной гирлянде 24 жёлтые лампочки. Это в 3 раза больше, чем зелёных. Сколько всего лампочек в ёлочной гирлянде?10. У Аллы 18 календариков. Это в 3 раза больше, чем у Кати. Сколько всего календариков у девочек?

(обобщение)

1. Нина купила 8 фруктовых творожков, а сырков в 2 раза меньше, чем фруктовых творожков. Сколько всего сырков и фруктовых творожков купила Нина?2. В булочную привезли 8 лотков со сдобами, а лотков с хлебом в 2 раза больше, чем лотков со сдобами. Сколько всего лотков с хлебом и сдобами привезли в булочную?3. В альбоме 10 фотографий с видами на море, а фотографий с видами на горы в 2 раза больше, чем фотографий с видами на море. Сколько всего в альбоме фотографий с видами на море и горы?3. В красной коробочке 8 кусков мыла, а в синей в 2 раза меньше, чем в красной коробочке. Сколько кусков мыла в двух коробочках?4. На строительстве дома работало 14 каменщиков, а маляров в 2 раза меньше, чем каменщиков. Сколько всего маляров и каменщиков работало на строительстве дома?5. На проспекте строители выстроили 8 новых домов, а на улице в 4 раза меньше, чем на проспекте. Сколько всего новых домов выстроили на улице и проспекте?6. С одного участка колхозного поля собрали 30 вёдер огурцов, а со второго в 3 раза меньше, чем с первого участка. Сколько вёдер огурцов собрали с двух участков колхозного поля?7. Туристы в первый день прошли 6 км, а во второй день в 3 раза меньше, чем в первый день. Сколько километров прошли туристы за два дня?8. Игорь съел 10 абрикосов, а Марина в 2 раза больше, чем Игорь. Сколько всего абрикосов съели дети?9. Одна тыква весит 8 кг. Это в 2 раза меньше, чем вторая. Сколько весят обе тыквы вместе?10. У Коли в коллекции 100 марок, а у Васи в 2 раза меньше, чем у Коли. Сколько всего марок у мальчиков?

Задачи на нахождение сторон геометрических фигур

1. Ширина прямоугольника 3 см. Чему равна его длина, если периметр равен 20 см? 2. Ширина прямоугольника 3 см. Чему равна его длина, если периметр равен 12 см?3. Ширина прямоугольника 3 см. Чему равна его длина, если периметр равен 10 см?4. Ширина прямоугольника 2 см. Чему равна его длина, если периметр равен 8 см?5. Ширина прямоугольника 8 см. Чему равна его длина, если периметр равен 32 см?6. Ширина прямоугольника 2 см. Чему равна его длина, если периметр равен 14 см?7. Ширина прямоугольника 1 см. Чему равна его длина, если периметр равен 8 см?8. Ширина прямоугольника 6 см. Чему равна его длина, если периметр равен 26 см?9. Ширина прямоугольника 7 см. Чему равна его длина, если периметр равен 16 см?10. Ширина прямоугольника 5 см. Чему равна его длина, если периметр равен 24 см?

Математика 6 класс

В 6ом классе появляется тема преобразования дробей в строчную запись. Что это значит? Например, дана дробь ½, она будет равна 0,5. ¼ = 0.25.

Примеры могут составляться в таком стиле: 0.25+0.73+12/31.

Примеры для тренировки:

Задание №1:

Задание №2:

Задание №3:

1. В двух классах в общем было 92 стула. Из первого класса перенесли 16 стульев во второй класс и потом количество их уровнялось. Сколько стульев было в первом и втором классе изначально?

2. В двух ящиках лежало 240 кг яблок. Из второго ящика в первый переложили 18 кг яблок. После количество яблок в первом и втором ящике уровнялось. Сколько килограмм яблок было изначально в первом и втором ящике.

3. Автомобилист выехал из города в деревню со скоростью равно 11,5 км/ч. Спустя 2,4 часа оттуда же и в том же направлении выехал автобус со скоростью 46 км/ч. Спустя какое время автобус догонит автомобиль?

История 1

Секунду назад я увидела, как пятилетний малыш уронил зеркало прямо посреди торгового зала. Осколки разлетелись по полу. Отец и мать опустились на пол возле мальчика и начали без лишних эмоций беседовать с ним о том, что он смог бы сделать сам, чтобы всё поправить.

Мать сказала малышу, что они могут спросить, есть ли в магазине щётка и совок, чтобы убрать осколки. Сын же, в свою очередь, спросил у отца, смогут ли они оплатить стоимость разбитого зеркала, если не будут покупать новые детские коньки, как планировали раньше.

Все консультанты застыли на месте, поражённые этой картиной, да и я почувствовала, что наше вмешательство будет лишним. Чёрт возьми! Как это, оказывается, легко! Случилось неприятное происшествие, и все трое в семье пытаются совместно найти выход из ситуации, ощущая взаимную помощь. Да, так и следует делать каждый раз. Но многие люди посмотрят на это в полном недоумении, ведь такое решение им в новинку.

История 2

В младших классах я дружила с одной девочкой и много раз сетовала моей маме на её поведение. Мне нравилось проводить время с ней, а она могла обмануть меня, часто вела себя неискренне, то уходила дружить с кем-то ещё, то опять приходила ко мне с предложением мира и дружбы.

И вот однажды эта девочка сказала мне, что нашей дружбе конец, и что она больше никогда не будет моей подругой. Помню, как прибежала домой вся в слезах, а моя мама процитировала высказывание, которое надолго отложилось у меня в памяти. «Судьба человека похожа на трамвай с пассажирами. Кто-то зайдёт, кто-то станет высаживаться. Кто-то будет ехать всю жизнь. А кто-то пробудет в этом трамвае совсем недолго. Но встретятся и такие люди, которых ты будешь вынуждена высадить сама, как кондуктор безбилетника».

История 3

Я помню как-то в раннем детстве, было ещё утро, а я поругался с моей мамой. Причина ссоры была пустяковая, но пока она провожала меня на уроки, я дулся и не проронил ни слова.

И вот мы с мамой вышли из автобуса. Перед тем как распрощаться и помахать рукой, мама повернулась ко мне и говорит: «Я тебя люблю». «А вот я тебя ненавижу», — вырвалось у меня от обиды. Удивительно, но мама не стала сердиться. Она просто тихонько ответила мне: «Не бросайся такими словами. Представь, что я вдруг попаду в аварию и это окажется наша последняя встреча. Разве тебе понравится, что самое последнее, что я услышу от тебя в этой жизни, это такая страшная фраза?».

Я давно уже вырос, но до сих пор, когда с кем-то прощаюсь, не допущу, чтобы мы разошлись, поругавшись или храня обиду. Ведь мы не можем быть уверены в том, увидим ли этого человека вновь.

Понравился наш контент? Подпишитесь на канал в .

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.

2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Пигментация и коричневые пятна

Составные задачи на нахождение неизвестного уменьшаемого

1.  Для уроков труда купили цветной бумаги. На поделки истратили 6 наборов бумаги по 10 листов в каждом наборе и осталось ещё 10 листов. Сколько листов цветной бумаги было первоначально?2. В санаторий привезли муку. Из 49 кг муки испекли булочки, и осталось 4 мешка муки по 9 кг в каждом. Сколько килограммов муки привезли в санаторий?3. После того как продали 7 мотков проволоки по 10 м в каждом, в магазине осталось 30 м проволоки. Сколько метров проволоки было в магазине изначально?4. Школьники должны были окапывать деревья. Не пришли 3 человека, и окапывали деревья 2 бригады по 8 человек. Сколько человек должны были окапывать деревья?5. В школу привезли билеты в цирк. Их продали 2 классам по 10 билетов в каждом классе, и осталось ещё 5 билетов. Сколько билетов привезли в школу?6. В магазин привезли помидоры. За день продали 29 кг помидоров и осталось 2 ящика помидоров по 8 кг в каждом. Сколько килограммов помидоров привезли в магазин?7. У учителя были проверочные работы. Он раздал 10 ученикам по две проверочные работы и у него осталось 20 работ. Сколько проверочных работ было у учителя?8. Бабушка купила мыло. Она подарила внукам 3 коробки мыла по 6 кусочков в каждой коробке, и у неё осталось ещё 4 кусочка мыла. Сколько кусочков мыла купила бабушка?9. У школьников были клубни георгинов. Они разбили около школы 2 клумбы, посадили на них по 9 клубней, и у них осталось ещё 18 клубней георгинов. Сколько клубней георгинов было у школьников?10. Серёже подарили марки. Он разместил их на 6 страницах кляссера по 10 марок на каждой странице, и у него осталось еще 32 марки. Сколько марок подарили Серёже?

Примеры по математике для 3 класса

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель начальных классов

Курс повышения квалификации

Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-426342

Дистанционный курс «Обучающиеся с ОВЗ: Особенности организации учебной деятельности в соответствии с ФГОС» от проекта «Инфоурок» даёт Вам возможность привести свои знания в соответствие с требованиями закона и получить удостоверение о повышении квалификации установленного образца (72 часа).

Подать заявку на курс

Похожие материалы

Вам будут интересны эти курсы:

Составные задачи на нахождение суммы двух произведений

1. У Алика на двух кассетах по 2 видеофильма и на пяти кассетах по 4 мультфильма. Сколько всего видеофильмов и мультфильмов у Алика?2. У Юли 2 альбома для акварели по 10 листов и 5 альбомов набросков по 8 листов. Сколько всего листов бумаги у Юли в альбомах?3. Ткачиха работала 6 дней по 8 ч и 4 дня по 7 ч. Сколько всего часов отработала ткачиха за одну декаду (10 дней)?4. В трёх скворечниках по 4 птенца, а в двух скворечниках по 5 птенцов. Сколько всего птенцов в этих скворечниках?5. Бабушка сварила 4 банки земляничного варенья по 3 л и 5 банок вишнёвого по 5 л. Сколько всего литров варенья сварила бабушка?6. Маша сорвала 7 стручков гороха по 6 горошин и 4 стручка по 5 горошин. Сколько всего горошин у Маши?7. Портниха на 7 кофт пришила по 3 пуговицы и на 3 кофты по 5 пуговиц. Сколько всего пуговиц пришила портниха? 8. Купили 4 коробки по 5 ёлочных игрушек и 3 коробки по 6 ёлочных игрушек. Сколько всего ёлочных игрушек купили?9. Марине на день рождения подарили 2 букета по 5 тюльпанов и 4 букета по 9 нарциссов. Сколько всего цветов подарили Марине?10. 2 болотные черепахи отложили по 11 яиц каждая, а 3 греческие черепахи по 8 яиц каждая. Сколько всего яиц отложили черепахи?

Симптомы заболевания сердца у женщин

Задачи по математике для 3 класса

Задача 2

• а) Как называют множество овец?
• б) Как называют множество лошадей?
• в) Как называют множество пчел, летящих вместе?
• г) Как называют множество футболистов, собравшихся вместе для игры? Какие еще командные игры ты знаешь?
• д) Как называют множество кораблей, плывущих вместе?
• е) Какие имеются названия для множеств военных?

Задача 4

Назови двух учеников твоего класса. Элементами какого множе-ства они являются? Принадлежат ли этому множеству портфели учеников?

Задача 6

На рисунке изображена семья Ивановых:

Покажи на этом рисунке множество детей и множество взрослых. Из каких элементов они состоят? Как будут звать Петю, когда он вырастет? Как будут звать Аню? Чьим отцом является Сергей Васильевич? Чьей бабушкой является Ирина Семеновна?

Задача 7

По какому признаку подобраны слова: роза, фиалка, гвоздика, василёк, тюльпан? Какие ещё элементы входят в это множество? Можно ли в пего включить сосну, барана, ромашку, шипы от розы? Какие цветы растут на клумбах? Какие растут в поле? Какие растут на лугу?

Задача 8

С каких деревьев взяты эти листья? Назови ещё 3 элемента множества деревьев. Всегда ли на деревьях есть листья? У всех ли деревьев есть листья?

Задача 9

Какое множество изображено на рисунке. В каких из этих плодов одно семечко или одна косточка, а в каких — много семян или косточек? Все ли плоды растут на деревьях? Что ещё растёт на дереве, кроме плодов?

• Реши задачи. Об элементах каких множеств в них идёт речь?

• а) Ласточка пролетает в час 40 км, а стриж — в 3 раза больше. Сколько километров в час пролетает стриж?
• б) Сосна живёт примерно 400 лет. Это на 250 лет больше, чем живёт липа. Сколько лет живёт липа?
• в) Для нормальной жизни рыбок скалярий им требуется но 3 л воды на каждую. Сколько рыбок могут жить в аквариуме, вмещающем 24 л воды?
• г) Масса пингвина-папы 42 кг, пингвина-мамы — 32 кг, а их детёныша — 8 кг. Какова масса всей пингвиньей семьи? На сколько папа тяжелее, чем мама с детёнышем вместе?

Пират нашёл клад из 900 монет. Чтобы побыстрее его унести, он положил 186 монет в шапку, 215 — в карман, 74 монеты запихнул в рот, 125 положил в правую ладонь, а 68— в левую. Сколько монет он не смог унести?

Составь программу действий и вычисли:

• а) 21 : 3 • 6 — (18 + 14) : 8
• б) 63 : (3 • 3) + (8 • 7 — 2) : 6

Два мальчика, Дима и Миша, отправились в булочную. По дороге они нашли 20 рублей. Сколько бы денег нашёл один Дима, если бы отправился в булочную?

На странице использованы задачи и задания из книги Л. Г. Петерсон «Математика. 3 класс. Часть1.» 2008г.
Ссылка на сайт автора: www.sch2000.ru

Пульсация

Первое понятие, которое необходимо ввести — пульс музыкального произведения.

Вы, наверное, замечали, что музыку часто описывают как нечто живое: весёлая, легкомысленная, задумчивая, решительная. И действительно, музыка имеет ряд качеств, характерных для живого организма, например такие как характер и настроение. Но главное, что в музыке, как и в живом организме бьется пульс. Вам наверняка доводилось бывать на концертах и хлопать в такт одновременно со всем залом. Это происходит именно потому, что люди чувствуют пульс музыки.

Как и человеческое сердце пульс может замедляться или ускоряться, но он бьётся равномерно и непрерывно на протяжении всего произведения.

Запомним: пульсация — это равномерность, которая обеспечивает музыкальное движение.

Как сделать разбор слова по составу и ничего не упустить

Чтобы выделить окончание, поизменяем слово: дом – дома – дому – домом. То, что изменяется, и есть окончание.

В слове может быть нулевое окончание: в данном случае оно не представлено, а при изменении слова появляется; нулевое окончание обязательно надо обозначить пустым квадратиком. В нашем примере слово с нулевым окончанием – дом.

Если трудно, напишите слова одно под другим, тогда будет проще заметить изменяющуюся часть. Вот так:

Дом

Дома

Дому

Домом

Если слово вообще не изменяется (наречие, деепричастие), у него вообще нет окончания – не нулевое, а нет, ведь слово не изменяется, так что окончание не появится – пустой квадратик рисовать не надо, это ошибка!

В сложных числительных бывает два окончания: пят-и-десят-и, пять-ю-десять-ю.

• Затем выделяем основу – все слово без окончания; для неизменяемых частей речи – просто все слово.
• Находим корень. Для этого подбираем однокоренные слова.

Можно опять писать слова одно под другим, если так удобнее:

Бездомный

Домашний

Дом

Повторяющаяся часть – это корень.

Не забываем, что существуют чередования, и обращаем внимание на значение корня: снег и –снеж- (снежок), пень и –пн- (пня) – это одни и те же корни, а –вод- (водичка) и –вод- (водитель) – как раз разные. В словах бывает два корня: пар-о-воз

В словах бывает два корня: пар-о-воз.

• Перед корнем находится приставка. Чаще она одна, но бывает и две, и даже три (по-на-вы-думывали)
• После корня – суффикс. Суффиксов часто бывает более одного. Чтобы понять, один это суффикс или несколько, надо попытаться подобрать «папу» слова – ближайшего предшественника в словообразовательной цепочке.

Пример:
горошинка – горошина; в этом слове два суффикса: -ин- и –к-

слезинка – слеза (нет слова слезина); один суффикс –инк-

Группировка нот

Группировкой называется объединение нот в группы. Это делается с одной простой целью – облегчить визуальное восприятие нот и ускорить разбор ритмического рисунка. Для сравнения приведу пример в виде номера телефона. Какой вариант легче воспринимать? Думаю, вы согласитесь, что второй:

Объединяться в группы могут только длительности с флажками, то есть длительности меньше четверти – восьмые, шестнадцатые и так далее. Когда они соединяются в группу, то флажки нот превращаются в горизонтальные линии — ребра. Сколько было флажков, столько будет и ребер у группы:

В группы могут объединяться ноты разной продолжительности, главное, чтобы все они были меньше четверти. Пусть вас не смущает разное количество флажков, это вовсе не мешает объединять ноты в группы:

Также паузы могут встраиваться в группу:

Группировка длительностей в такте

Рассмотрим пример группировки нот в самых популярных размерах: 2/4, 3/4, 4/4, 6/8.

В размерах 2/4, 3/4, 4/4 ноты объединяются в группы по счетным долям (они указаны в знаменателе размера) – в нашем случае это четверти. Группировать следует так, чтобы границы долей было отчетливо видно. Например, в размере 4/4 шестнадцатые ноты нужно группировать по четыре:

Не трудно посчитать, что каждая группа равна четвертной доле. В одном такте будет 4 таких группы.

А вот пример того, как группировать не следует:

Визуально воспринимать такую группировку нот чрезвычайно трудно, а читать с листа – невозможно.

Размер 4/4 — сложный и состоит из двух простых – 2/4 + 2/4. Поэтому иногда ноты в этом размере группируются не по долям, а в соответствии с составным простым размером. Получится две группы по две четверти. Как лучше сгруппировать ноты выбирает сам композитор, главное, чтобы это легко воспринималось глазами.

В размере 2/4 ноты объединяют в две группы, каждая из которых равна четверти:

Ниже приведен пример группировки в размере 3/4:

Ритмический рисунок не самый простой, но ноты сгруппированы таким образом, что сразу видно каждую долю и посчитать размер такта не составит труда.

В размерах 6/8, 9/8, 12/8 счёт осуществляется восьмыми нотами. Принцип группировки в таких размерах будет несколько другим. Эти размеры сложные трехдольные и, как вы уже знаете, состоят они из нескольких простых:

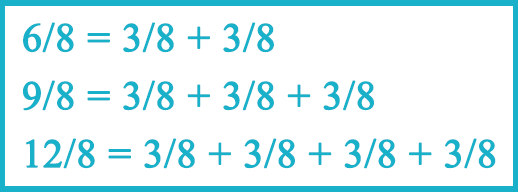
Группировать ноты в подобных случаях, следует опираясь на простой размер, из которого состоит сложный — в нашем случае это размер 3/8. Эти цифры служат нам подсказкой, говоря, что ноты нужно собирать в такие группы, где сумма длительностей будет равна трем восьмым. Например, в размере 6/8 (3/8+3/8) ноты нужно объединять в две группы по три восьмые в каждой.

Ритм может быть самым разнообразным, но каждая группа нот, все равно должна быть равны трем восьмым:

Группировка нот напрямую зависит от музыкального размера. Мы рассмотрели не все варианты группировки, но главное усвоить принцип и запомнить, что группировать нужно так, чтобы это было удобно читать.

Статья понравилась189Статья не понравилась101

Заключение

А сейчас посмотрите джазовую пьесу «Take Five«, записанную квартетом «The Dave Brubeck Quartet» в 1959 году. это был первый джазовый сингл, разошедшийся в более чем миллионе экземпляров. Автор пьесы — Paul Desmond, саксофонист квартета. Написана эта музыка в достаточно необычном ритме 5/4. Именно отсюда и идет ее название.

https://youtube.com/watch?v=tT9Eh8wNMkw%3F

Как сделать разбор сложного предложения

Чтобы составить схему сложного предложения, нужно сначала найти все его основы. Это поможет понять, сколько в нем частей, после этого можно будет найти, как они между собой связаны. Рассмотрим это на примере.

В этом предложении две основы (ребята гуляли, снег пошел), которые соединены между собой интонацией, что на письме отражается в виде запятой. Союза между этими частями нет.

В сложном предложении не обязательно должно быть строго две грамматических основы: их может быть три и даже больше.

В основном порядок частей в сложном предложении последовательный: сначала идет главная часть, за ней следует та, которая связана с ней по смыслу. В предложениях, которые связаны интонацией и представляют собой просто перечисление событий, часто нет главной и присоединенной части – их порядок можно поменять местами и смысл предложения от этого совершенно не изменится.

Это легко понять, если сравнить два сложных предложения с одинаковыми основами, которые просто переставлены местами:

• Веет ветер, моросит дождик.
• Моросит дождик, веет ветер.

Очевидно, что от перестановки частей смысл предложения совершенно не поменялся: оно рассказывает о погоде, описывая ее с разных сторон.

Такой принцип роднит сложные предложения с максимально простой структурой с примерами на сложение, где от перестановки мест не изменяется итоговая сумма, что говорит о том, что язык в какой-то степени математичен.

Алгоритм разбора любого предложения, в котором две и больше основ, одинаковый: нужно найти эти основы и определить, соединены ли они только интонацией, то есть знаком препинания, или в установлении связи между ними участвовал союз.

Что мы узнали?

Определение сложного предложения само по себе достаточно простое: это такая единица языка, в которую входит не одна грамматическая основа, а несколько (как минимум две и больше). Эти части могут соединяться только интонацией (знаком препинания) или интонацией и союзом. Чтобы разобрать сложное предложение, нужно сначала найти все его основы, а потом определить, каким образом они соединены между собой. Это достаточно простой и понятный алгоритм.

1. Вопрос 1 из 10

Начать тест(новая вкладка)

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.

После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Примеры на порядок действий | 3 класс

Тренируйте своих третьеклассников с нами!

Мозги напрягаем, примеры решаем!

Примеры в несколько действий

8+60:3	80+12:2-21
25-2×2	8×4-15:5
(67+3):2	4×5+(82-71)
6×(8-2):9	59+7×(6-4)
5+80:8	(32+4×6):2
22-2×6	48+68:4-60
3×(8-6)	7×9-15:5
(92+8):2	3×9+(52-48)
3×(8-2):9	58+3×(6-2)
4×3+24:7	29+5×7):8

3+12:2	96+18:9-76
55-2×3	5×9-24:4
9×(5-3)	7×5+(80-55)
(41+3):4	85+3×(6-2)
9×(8-5):3	(64+4×8):2
4+40:8	74+24:3-75
48-5×9	3×4-54:9
4×(4-2)	7×6+(32-13)
(86+5):7	74+2×(7-5)
5×(6-4):2	(60+4×3):6

5+12:2	60+39:3-61
22-4×5	6×2-28:4
6×(8-2)	9×4+(71-17)
(54+9):9	24+6×(5-2)
2+20:4	5×(9-7):2
65-4×4	(51+9×3):6
9×(9-2)	70+72:9-75
(21+9):3	9×8+(45-22)
9×2-44:4	50+4×(8-5)
5×(7-4):3	(74+2×5):3

5+48:8	56+72:2-23
95-6×2	9×8-28:2
3×(8-3)	4×9+(47-12)
(73+5):6	76+6×(9-5)
4×(7-2):5	(36+4×7):2
8+80:5	78+88:4-21
82-4×2	2×7+(70-30)
4×(5-2)	75+2×(8-6)
(36+9):5	6×(9-4):5
9×5-96:6	(24+6×7):3

Нравится Загрузка…

Заключение

Количество богатых белком продуктов в рационе больного фенилкетонурией должно быть резко ограничено.

Фенилкетонурия – тяжелое заболевание, которое без квалифицированной помощи имеет крайне неблагоприятный прогноз. Лечение таких детей сопряжено с определенными сложностями. Оно требует своевременного начала и постоянного медицинского контроля. Разные пациенты по-разному реагируют на диетотерапию, что в первую очередь зависит от формы болезни. У большей части из них удается добиться удовлетворительных результатов лечения и сохранения интеллекта (обычно при классическом течении болезни). При позднем начале терапии (если ребенку больше 1 года) она не эффективна.

О фенилкетонурии в программе «Жить здорово!» с Еленой Малышевой: