Онлайн примеры по математике

Склонение существительных по падежам

В русском языке существует шесть падежей – один прямой (именительный) и пять косвенных. Изменение имен существительных по падежам осуществляется с помощью системы падежных окончаний (флексий).

Примеры падежей существительных в таблице:

Падеж	Вопросы к падежам	Примеры существительных
Ед. число	Мн. число
Именительный	Кто? Что?	Приятель, ветка, озеро	Приятели, ветки, озера
Родительный	Кого? Чего?	Приятеля, ветки, озера	Приятелей, веток, озер
Дательный	Кому? Чему?	Приятелю, ветке, озеру	Приятелям, веткам, озерам
Винительный	Кого? Что?	Приятеля, ветку, озеро	Приятелей, ветки, озера
Творительный	Кем? Чем?	Приятелем, веткой, озером	Приятелями, ветками, озерами
Предложный	О ком? О чем?	О приятеле, о ветке, об озере	О приятелях, о ветках, об озерах

Несклоняемые существительные не имеют падежных форм. У таких слов падежная принадлежность выражается не грамматически (через окончания), а синтаксически (через слова, с которыми они согласуются).

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Математика и арифметика

Математика и арифметика тесно связанные понятия, а вернее арифметика – раздел математики, работающий с числами и вычислениями (действиями с числами).

Арифметика – основной раздел, а значит и основа математики. Основа математики – важнейшие понятия и операции, составляющие базу, на которой строятся все последующие знания. В число главных операций входят: сложение, вычитание, умножение, деление.

Арифметика, как правило, изучается в школе с самого начала обучения, то есть. с первого класса. Дети осваивают базу математики.

Сложение – это арифметическое действие, в процессе которого складываются два числа, а их результатом будет новое – третье.

Формула сложения выражается так: a + b = c.

Вычитание – это арифметическое действие, в процессе которого из первого числа вычитается второе число, а итогом будет третье.

Формула сложения выражается так: a — b = c.

Умножение – это действие, в итоге которого находится сумма одинаковых слагаемых.

Формула такого действия имеет вид: a1+a2+…+an=n*a.

Деление– это разбивание на равные части какого-либо числа или переменной.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Прямое значение слова

Слова нашей речи назы­ва­ют пред­ме­ты, их при­зна­ки и дей­ствия. Однозначные сло­ва непо­сред­ствен­но соот­но­сят­ся с объ­ек­том дей­стви­тель­но­сти, напря­мую назы­ва­ют пред­мет, его при­знак или про­цесс дей­ствия. Это пря­мое зна­че­ние сло­ва.

В пото­ке речи такие сло­ва сра­зу вызы­ва­ют пред­став­ле­ние о том, что они назы­ва­ют. Их зна­че­ние не зави­сит от кон­тек­ста, напри­мер:

Большинство слов рус­ско­го язы­ка высту­па­ют в пря­мом зна­че­нии в соб­ствен­ном смыс­ле.

Примерыдочь, дом, тра­ва, веж­ли­вый, огром­ный.ОпределениеПрямое зна­че­ние сло­ва — это его основ­ное лек­си­че­ское зна­че­ние без допол­ни­тель­ных оттен­ков.

Как правильно научить ребёнка решать задачи

Если ребёнок только начинал осваивать навык решения задач, приучите его придерживаться определённого алгоритма.   

1. Внимательно читаем условия  

Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.

Особую сложность представляют задачи с косвенным вопросом, например:

«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.        

2. Делаем описание задачи

В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе. 

Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.  

Формы краткой записи условий задач / shkola4nm.ru‍

3. Выбор способа решения

Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно. 

Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых. 

Ребёнок должен знать способы получения неизвестных данных из двух известных:

• слагаемое = сумма − слагаемое
• вычитаемое = уменьшаемое − разность
• уменьшаемое = вычитаемое + разность
• множитель = произведение ÷ множитель
• делитель = делимое ÷ частное
• делимое = делитель × частное

После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем. 

4. Формулировка ответа

Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.

Задание из базового курса алгебры домашней онлайн-школы «Фоксфорда», 7 класс‍

Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.   

5. Закрепление результата

Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.

Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов. 

В нашей онлайн-школе, помимо уроков, ученики могут закреплять  свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения. 

Аналитическая геометрия

Пример 16. Уравнение плоскости, проходящей через точку перпендикулярно вектору

Написать уравнение плоскости, проходящей через точку M перпендикулярно вектору .Дано:
Координаты точек: M(2, 5, -3), M₁(7, 8, -1) и M₂(9, 7, 4).Найти:
Уравнение плоскости, проходящей через точку M перпендикулярно вектору .

Решение:
В качестве нормального вектора плоскости выбираем вектор = {x₂-x₁, y₂-y₁, z₂-z₁} = {9-7, 7-8, 4-(-1)} = {2, -1, 5}.

Уравнение плоскости, проходящей через точку M(x, y, z) перпендикулярно вектору = {A, B, C}, имеет вид .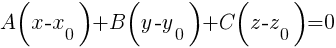

Составляем уравнение плоскости с нормальным вектором = {2, -1, 5}, проходящей через точку M(2, 5, -3):.

Ответ: .

Пример 17. Уравнение плоскости «в отрезках»

Какие отрезки отсекает на осях координат плоскость?Дано:
Уравнение плоскости: 2x – 4y + 6z – 12 = 0.Найти:
Отрезки, которые отсекает на осях координат плоскость.a, b, c — ?

Решение:
Приведем общее уравнение плоскости к виду уравнения «в отрезках»:

Уравнение — это уравнение плоскости «в отрезках». Параметры представляют собой координаты точек пересечения плоскости с координатными осями и равны (с точностью до знака) отрезкам, отсекаемым плоскостью на координатных осях.

Применяя вышеприведенное к уравнению 2x – 4y + 6z –12 = 0, получим:.

Отрезки, отсекаемые на осях, равны a = 6, b =−3, c = 2.
Отрицательный знак перед b показывает, что плоскость пересекает отрицательную полуось Oy.

Задачи по теме «Уравнение плоскости в пространстве»

Задача 1. Составить канонические уравнения прямой:

Решение:
Для составления канонического или параметрического уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты вектора, коллинеарного прямой.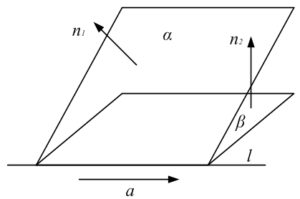
Так как прямая является линией пересечения двух плоскостей, ее направляющий вектор а параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям n₁ и n₂ к данным плоскостям. В таком случае он коллинеарен векторному произведению [n₁, n₂].n₁ = (2; 1; -5), n₂ = (5; 3; 8), [n₁, n₂] = (23; -41; 1).
Итак, (l; m; n) = (23; -41; 1).

Найдем точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить из системы уравнений, задающей пересекающиеся плоскости.

Примем для удобства вычислений z = 0, тогда для точки A={х; у; 0}x = -4; y = 11; A = {4; 11; 0}.

Cоставим канонические уравнения данной прямой:.

Ответ: .

Задача 2. Составить уравнение плоскости, проходящей через прямую k: и точку B = {2; -3; 1}.

Решение:
Так как точка А = {-3,5,-1} принадлежит плоскости, значит вектор AB параллелен плоскости.
Так как данная прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости.
Значит, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Так как прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости. При d = 0 из уравнений прямой получаем: — координаты точки А, принадлежащей прямой и соответственно плоскости.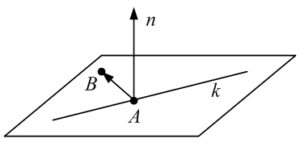

Получается, что вектор AB = (5; -8; 2) параллелен плоскости. Значит, нормаль n к плоскости коллинеарна векторному произведению = (-6; -9; -21).
Примем n = (2; 3; 7) и составим уравнение плоскости, проходящей через точку B перпендикулярно n: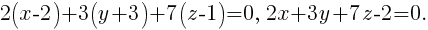

Ответ: 2x + 3y + 7z – 2 = 0.

Задача 3.Написать уравнение плоскости, которая проходит через три точки с координатами N₁(x₁, y₁, z₁), N₂(x₂, y₂, z₂), N₃(x₃, y₃, z₃).

Решение:
Предположим, что какая нибудь, находящаяся на плоскости точка N, имеет координаты (x, y, z). Для этого случая уравнение плоскости примет вид:
(r-r, a, b) = 0,
гдеr = (x, y, z);r = (x₁, y₁, z₁);
базисные векторы (смотрите рисунок) соответственно равны и .

Если записать смешанное произведение в виде определителя, то получим необходимое уравнение плоскости:

Ответ:

Обучение арифметике

Обучение арифметике производится в стенах школы. С первого класса дети начинают изучение базового и главного раздела математики – арифметики.

Сложение чисел

Сложение – это сумма двух или нескольких чисел. Например, 2 + 3 = 5, и графически это можно представить так:

Большие число делиться на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Итак, если мы прибавляем 4 к 7, то 4+7=10+1, то есть 1 десяток и 1 единица. Если складывая числа в одном разряде (единицах, например) у вас число больше 10, но меньше 20, то в десяток вы добавляете единицу, а остальное оставляете на месте единиц.

Еще один пример: 8+9, получаем 10+7, значит в десятки мы добавляем 1, а на место единиц записываем 7, получаем 17.

Вычитание чисел

Вычитание – обратная операция сложению. Например, из 6 нужно вычесть 5. 6-5=1, 6 больше числа 5 на единицу, значит, и ответ будет единицей. Можно для проверки произвести сложение 1+5=6.

Большое число делится на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Если вычитать единицы, то все легко и просто. Но допустим пример: 14 — 7. В числе 14: 1 – десяток, а 4 – единицы. Один десяток – 10 единиц. Тогда получаем 10 + 4 — 7, сделаем так: 10 — 7 + 4, 10 — 7 = 3, а 3 + 4 = 7. Ответ найден верно!

Рассмотрим пример 23 — 16. Первое число 2 десятка и 3 единицы, а второе 1 десяток и 6 единиц. Представим число 23 как 10 + 10 + 3, а 16 как 10 + 6, тогда представим 23 — 16 как 10 + 10 + 3 — 10 — 6. Тогда 10 — 10 = 0, останется 10 + 3 — 6, 10 — 6 = 4, тогда 4 + 3 = 7. Ответ найден!

Аналогично делается с сотнями и тысячами/

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Деление чисел

Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Ускоряем устный счет, НЕ ментальная арифметика

Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Формулы приведения задаются в виде таблицы:

Камера калькулятор — решение задач по математике

Очередной калькулятор с камерой может быть полезен для решения математических задач и не только. В нём сосредоточено большое количество функций, которые будут полезны в разных сферах деятельности. В дополнение в нём можно найти научный калькулятор, который может быть использован инженерами и студентами. Калькулятор уравнений может решать уравнения и неравенства разной сложности. В результатах отображает графики.

Ссылка: https://play.google.com/store/apps/details?id=math.scientific.calculator.camera.plus

Приложение «Калькулятор с камерой» работает через внешнюю камеру смартфона. Загрузив и запустив его, необходимо навести объектив на пример и нажать на кнопку для создания фото. На окне результатов можно переключаться при помощи вкладок, чтобы посмотреть графики и варианты решения примеров и уравнений.

Правила пунктуации со словом «например»

Для правильной постановки знаков препинания необходимо также принимать во внимание контекст и смысл фразы целиком:

1. Со значением уточнения, пояснения слово отделяется при помощи запятых с обеих сторон, если находится в середине предложения. При позиции в начале или в конце – одной запятой.
2. Слово «например» в начале обособленного оборота запятой от этого оборота не отделяется.
3. Когда обособленный оборот заключен в скобки, то запятая после «например» ставится.
4. Если за словом «например» следуют однородные члены предложения, впереди оно отделяется запятой, а после него ставится двоеточие.
5. В сочетании «как например» запятая не ставится в случае последующего перечисления.
6. Если перечисление отсутствует, то «например» выделятся запятыми с обеих сторон.

Примеры предложений

1. Завтра, например, ожидаются осадки.
2. Существуют разные виды спорта. Например, теннис.
3. Я люблю зелень. Петрушку, например.
4. В некоторых городах, например, в Сиднее, проходили Олимпийские игры.
5. В некоторых городах (например, в Сиднее) проходили Олимпийские игры.
6. Я посетил разные страны, например, Италию, Францию, Канаду, Тайланд.
7. Некоторые фрукты, как, например, лимон, апельсин, лайм… называются цитрусовыми.
8. Существуют гуманитарные дисциплины, как, например, история.

Процесс счёта

Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.

Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.

Подробное решение примеров

В любой момент работы с тренажером вы можете перейти в разделу «Подробного решения примера», если обычной подсказки в виде верного ответа вам не достаточно. Для этого кликните на соответствующую иконку сверху, либо перелестнув страницу вниз.

Здесь вы сможете посмотреть подробное решение примера с дробями со всеми преобразованиями, сокращениями и упрощениями.

Дополнительная информация

Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:

домен сайта + раздел приложения + кодировка данного режима

например: matematika.club/drobi/#60101

Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.

Порядковый счёт

Количественный счёт (ответ на вопрос «сколько») ребята обычно усваивают между делом и закрепляют на занятиях по математике в детском саду. С порядковым  (ответ на вопрос «который по счёту») дело обстоит сложнее. Обычно ему внимания уделяют мало или совсем не уделяют.

Нам поможет познакомиться с порядковым счётом стихотворение Ирины Гуриной, которое так и называется

ПОРЯДКОВЫЙ СЧЁТ

На поляне у реки Жили-были мотыльки. Братья разноцветные Как фантики конфетные.

Первый — красный, как рябина, Словно капелька рубина.	А второй — небесно-синий В белых брызгах, будто иней.	Третий — жёлтый, как лимон, Светом солнца окрылён.
А четвёртый — белоснежный, Лепесток ромашки нежный.	Пятый — рыжий, как лиса, Полосатый, как оса.	В синих точках брат шестой, Бело-красно-золотой.
А седьмой — совсем лиловый, Лишь с полоской бирюзовой.	Брат восьмой — чуть-чуть зелёный, Словно океан солёный.	А девятый — красный в точках, Белых ромбах и кружочках.
	Пёстрый весь, как конфетти, Брат десятый, к нам лети!

Вы можете распечатать картинки наши и выкладывать их по порядку, а можете нарисовать с ребёнком собственные. Возможно, это будет даже лучше. Закрепляя порядковый счёт, расставляйте по порядку любые предметы, например, игрушки. Который по порядку слоник, лисичка…

Падежи существительных. Падежные предлоги

Именительный падеж

Именительный падеж упо­треб­ля­ет­ся для наиме­но­ва­ния пред­ме­тов. Это исход­ная, началь­ная фор­ма суще­стви­тель­но­го, кото­рая отве­ча­ет на вопро­сы:

• кто? — бабушк а , мастер , отец ;
• что? — тишин а , дом , счасть е , радость .

Именительный падеж все­гда упо­треб­ля­ет­ся без пред­ло­га и назы­ва­ет­ся пря­мым паде­жом в отли­чие от осталь­ных, нося­щих назва­ние кос­вен­ных. В име­ни­тель­ном паде­же суще­стви­тель­ное высту­па­ет в роли под­ле­жа­ще­го в пред­ло­же­нии или имен­ной части ска­зу­е­мо­го.

Вася — мой млад­ший брат .

Родительный падеж

• нет (кого?) бабушк и , мастер а , отц а ;
• нет (чего?) тишин ы , дом а , счасть я , радост и .

Все кос­вен­ные паде­жи (кро­ме пред­лож­но­го) могут упо­треб­лять­ся как с пред­ло­га­ми, так и без них, напри­мер:

нет (чего?) дома — оста­но­вил­ся (у чего?) у дома.

Предлоги уточ­ня­ют зна­че­ние паде­жей. Так, с роди­тель­ным паде­жом для обо­зна­че­ния отсут­ствия пред­ме­та, ука­за­ния места, при­чи­ны, цели упо­треб­ля­ют­ся пред­ло­ги:

Например:

• Дам (кому?) бабушк е , мастер у , отц у ;
• дам (чему?) тишин е , дому, счасть ю , радост и .

С датель­ным паде­жом упо­треб­ля­ют­ся пред­ло­ги:

• Подойти к мате­ри;
• посту­пить соглас­но пра­ви­лам;
• идти навстре­чу вет­ру;
• дей­ство­вать напе­ре­кор судь­бе.

Винительный падеж

Винительный падеж суще­стви­тель­но­го обо­зна­ча­ет объ­ект дей­ствия и отве­ча­ет на вопро­сы: кого? что?

• Вижу (кого?) бабушк у , мастер а , отц а ;
• вижу (что?) тишин у , дом , счасть е , радость .

С суще­стви­тель­ны­ми в фор­ме вини­тель­но­го паде­жа в зна­че­нии объ­ек­та, вре­ме­ни, места, уступ­ки упо­треб­ля­ют­ся пред­ло­ги:

• Вернуться спу­стя год;
• рас­ска­зать про орла;
• прой­ти сквозь пла­мя;
• пере­сту­пить через сту­пень­ку;
• вый­ти, несмот­ряна ливень.

Предлоги «в», «на», «за», «под» в фор­ме вини­тель­но­го паде­жа суще­стви­тель­но­го рас­кры­ва­ют направ­лен­ность на объ­ект дей­ствия:

Творительный падеж

• Горжусь (кем?) бабушк ой , мастер ом , отц ом ;
• любу­юсь (чем?) тишин ой , дом ом , счасть ем , радость ю .

С этим паде­жом в зна­че­нии сов­мест­но­сти, места, при­чи­ны упо­треб­ля­ют­ся пред­ло­ги:

• при­е­хать с дру­гом;
• парить над полем;
• оста­но­вить­ся перед вок­за­лом;
• поса­дить за домом;
• дей­ство­вать соглас­но с рас­по­ря­же­ни­ем;
• я вме­сте с бра­том;
• в свя­зи с непо­го­дой;
• прой­ти меж­ду ряда­ми.

Предложный падеж

Предложный падеж суще­стви­тель­но­го обо­зна­ча­ет объ­ект раз­мыш­ле­ний и отве­ча­ет на вопро­сы: о ком? о чём?

• забо­чусь о ком? о бабушк е , о мастер е , об отц е ;
• рас­ска­жу о чём? о тишин е , о дом е , о счасть е , о радост и .

Существительное в фор­ме пред­лож­но­го паде­жа, как гово­рит его назва­ние, упо­треб­ля­ет­ся толь­ко с пред­ло­га­ми:

Предложные фор­мы суще­стви­тель­ных обо­зна­ча­ют объ­ект дей­ствия или место:

Обратим вни­ма­ние, что оду­шев­лен­ные суще­стви­тель­ные отве­ча­ют на вопро­сы: кто? кого? кому? кем? о ком?

Неодушевленные суще­стви­тель­ные отве­ча­ют на падеж­ные вопро­сы: что? чего? чему? чем? о чём?

Онлайн-калькулятор дробей по изображению

Нередко знакомство с дробями в школе у подростков вызывает шок. Во всех начальных школах по программе они следуют сразу же за обычной и более понятной все математикой. Детям бывает не легко понять, как можно целое число разделить на 20 частей.

Уравнения с дробями

Материал усваивается со временем. А для решения более трудных примеров можно применять «Калькулятор дробей». С его помощью можно решать проценты со скобками, десятичные дроби. Каждый пример приводится пошагово. Поэтому он поможет понять, как такие задачи могут быть выполнены.

Калькулятор дробей

Калькулятором дробей можно решать как простые, так и сложные примеры с преобразованием дробей в десятичные числа по фотографии. Показывая варианты выполнения примеров, приложение делает это в простой и понятной форме.

В примерах поддерживаются скобки и задания с процентами. В программе можно работать с большими числами, будет полезен для школьников 5 и 6 классов. Не дробные (в периоде) результаты показывает по аналогии с калькулятором.

Кроме этого интерфейс приложения может быть настроен пользователем. Выбирайте темы для калькулятора и изменяйте расположение кнопок управления. Калькулятор может быть установлен на устройства Android 4.1 или выше.

Вопросы и ответы. Примеры предложений:

С обычными глаголами

Чтобы образовать вопросы в Present Simple с обычными глаголами, мы также добавляем вспомогательные глаголы do и does. В данной статье мы рассмотрим два типа вопросов — общие и специальные.

Общие вопросы начинаются с do или does, в зависимости от лица (на русский язык do и does не переводятся). Такие вопросы требуют ответа «Да» или «Нет». Примеры:

• Do you speak English? (Вы говорите по-английски?) — Yes, I do. (Да) / No, I don’t. (Нет)
• Does he play tennis? (Он играет в теннис?) — Yes, he does. (Да) / No, he doesn’t. (Нет)

Специальные вопросы начинаются с вопросительных слов Where, What, When, Why, How и тд, а затем повторяют структуру общих вопросов. Пример:

When do you read books? (Когда ты читаешь книги?) — In the evening. (Вечером)

Отвечать на такие вопросы можно полным предложением или кратко. Пример:

Where does he play football? (Где он играет в футбол?) — He plays football on the stadium. (полный ответ) / On the stadium. (краткий ответ).

Примеры вопросительных предложений в Present Simple с обычными глаголами:

Вопрос	Перевод	Ответ	Перевод
Do you live in the city?	Ты живешь в городе? / Вы живете в городе?	Yes, I / we do. / No, I / we don’t.	Да / Нет
Does she play the piano?	Она играет на пианино?	Yes, she does. / No, she doesn’t.	Да / Нет
Does Tim sleep well?	Тим хорошо спит?	Yes, he does. / No, he doesn’t.	Да / Нет
Do they write letters?	Они пишут письма?	Yes, they do. / No, they don’t.	Да / Нет
Does he drive a car?	Он водит машину?	Yes, he does. / No, he doesn’t.	Да / Нет
Where do you live?	Где вы живете?	In Sydney.	Мы живем в Сиднее.
How do you make pasta?	Как ты готовишь пасту?	I use Mom’s recipe.	Я использую мамин рецепт.
What do you do in the morning?	Что ты делаешь утром?	I take a shower and make breakfast.	Я принимаю душ и готовлю завтрак.
Where does she go at 4 pm?	Куда она ходит в 4 часа дня?	To the swimming pool.	В бассейн.
What time do they go to sleep?	Во сколько они ложатся спать?	At 11 pm.	В 11 вечера.

С глаголом to be

С глаголов to be вопросы строятся простой перестановкой слов. Чтобы образовать общий вопрос, глаголы am, is, are ставятся вначале, то есть меняются порядком с подлежащим. Пример:

• He is a doctor. (Он врач.) — Is he a doctor? (Он врач?)
• They are builders. (Они строители.) — Are they builders? (Они строители?)

Специальные вопросы начинаются с вопросительных слов, а затем повторяют структуру общего вопроса. Пример:

• Why is he sad? (Почему он грустный?)
• When is your birthday? (Когда у тебя день рождения?)
• Where is the bag? (Где сумка?)

Примеры вопросительных предложений в Present Simple с глаголом to be:

Вопрос	Перевод	Ответ	Перевод
Are you on holiday?	Вы на каникулах? / Ты на каникулах?	Yes, we are. / No, we aren’t. / Yes, I am. / No, I am not.	Да / Нет
Is the apple red?	Яблоко красное?	Yes, it is. / No, it isn’t.	Да / Нет
Are they tall?	Они высокие?	Yes, they are. / No, they aren’t.	Да / Нет
Is Polly funny?	Полли смешная?	Yes, she is. / No, she isn’t.	Да / Нет
Are we happy?	Мы счастливы?	Yes, we are. / No, we aren’t.	Да / Нет
What color is the car?	Какого цвета машина?	It’s blue.	Она синяя.
How are you?	Как ты? Как дела?	I’m fine.	Хорошо.
Where is the post office?	Где почта?	It’s opposite the bank.	Она напротив банка.
Why are they tired?	Почему они устали?	They worked a lot.	Они много работали.
What time is your class?	Во сколько у тебя урок?	At 1 pm.	В час дня.

И напоследок, чтобы закрепить материал, советую вам посмотреть видео по всем трем видам предложений в Present Simple:

Успехов вам в изучении!

Читать далее:

Тест на Present Simple с ответами (для начинающих)Тест на Present Simple с ответами (для продолжающих)

Что поможет ребёнку решать задачи

В заключение расскажем о том, как сделать процесс решения задач проще и интереснее. 

• Для того чтобы решать задачи, необходимо уметь считать. Поэтому прежде всего следует научить ребёнка решать примеры с дробями, простые уравнения и таблице умножения.   
• Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке. 
• Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.   

<<Блок перелинковки>>

После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.

Решение уравнений с дробью

Для решения подобных заданий к нашему алгоритму придется добавить еще один шаг. Но для начала я напомню наш алгоритм:

1. Раскрыть скобки.
2. Уединить переменные.
3. Привести подобные.
4. Разделить на коэффициент.

Увы, этот прекрасный алгоритм при всей его эффективности оказывается не вполне уместным, когда перед нами дроби. А в том, что мы увидим ниже, у нас и слева, и справа в обоих уравнениях есть дробь.

Как работать в этом случае? Да всё очень просто! Для этого в алгоритм нужно добавить ещё один шаг, который можно совершить как перед первым действием, так и после него, а именно избавиться от дробей. Таким образом, алгоритм будет следующим:

1. Избавиться от дробей.
2. Раскрыть скобки.
3. Уединить переменные.
4. Привести подобные.
5. Разделить на коэффициент.

Что значит «избавиться от дробей»? И почему выполнять это можно как после, так и перед первым стандартным шагом? На самом деле в нашем случае все дроби являются числовыми по знаменателю, т.е. везде в знаменателе стоит просто число. Следовательно, если мы обе части уравнения домножим на это число, то мы избавимся от дробей.

Пример №1

\

\

Давайте избавимся от дробей в этом уравнении:

\

Обратите внимание: на «четыре» умножается все один раз, т.е. если у вас две скобки, это не значит, что каждую из них нужно умножать на «четыре»

Запишем:

\

Теперь раскроем:

\

\

Выполняем уединение переменной:

\

Выполняем приведение подобных слагаемых:

\

\

\

Мы получили окончательное решение, переходим ко второму уравнению.

Пример №2

\

Здесь выполняем все те же действия:

\

\

\

\

\

\

\

Задача решена.

Вот, собственно, и всё, что я хотел сегодня рассказать.