Как объяснить ребенку деление?

Что нужно знать, что бы научиться делить

Прежде, чем приступить к делению, нужно убедиться в том, что ребенок усвоил азы математики – сложение, вычитание.

Надо объяснить ему основы умножения и проверить знание таблицы умножения. Необходимо убедиться, как он выучил разряды чисел.

Без этих основ вряд ли получится проводить арифметические операции с числами

Математика не терпит пробелов в знаниях, поэтому важно вложить этот принцип в голову ребенка с раннего возраста. Даже если какая-то часть материала была пропущена по причине болезни или иного отсутствия на уроке, материал должен быть выучен

Пробелы в знаниях повлекут за собой трудности в решении задач, примеров, а в старших классах и проблемы в изучении других дисциплин.

На самом деле вам нужно только знать таблицу на 6

Умножение коммутативно. Если вы знаете 7 x 6 = 42, знайте, что 6 x 7 = 42, если 8 x 6 = 48, то  6 x 8 = 48, и если вы знаете 8 x 7 = 56, вы знаете, что 7 x 8 = 56, и вы будете уметь сократить количество фактов, оставшихся для изучения, до последних шести, упомянутых в начале. Вы можете даже обнаружить, что уже выучили некоторые из этих последних шести, просто прочитав эту статью.

6 х 6 = 36
7 х 6 = 42
8 х 6 = 48
7 х 7 = 49
8 х 7 = 56
8 х 8 = 64

Если вы прочитаете эту статью 2 или 3 раза, вы удивитесь, сколько вы сохраните. Вот и финальная сетка, по-настоящему разделенная и завоеванная!

Я разработал этот метод, когда писал свой блог по математике на GCSE, и мои дети обнаружили, что он им помог. Как вы думаете? Знаете ли вы какие-нибудь другие приемы, которые я должен включить в свой математический блог?

Как правильно делить числа в столбик: алгоритм деления

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

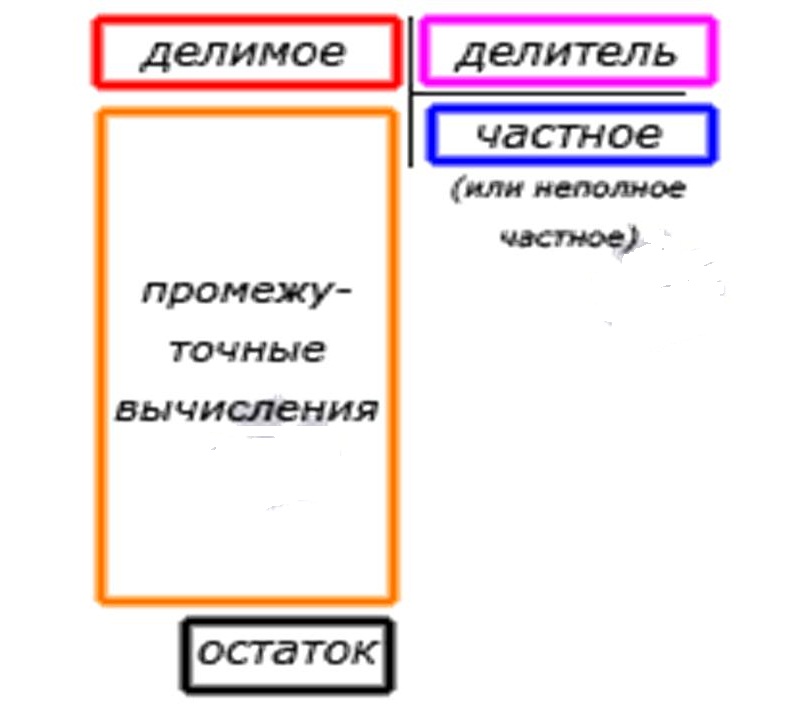
• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Деление столбиком

Лишь после того, как ученик освоил и хорошо запомнил предыдущие способы, можно переходить к делению столбиком, с остатком или без него.

Вначале необходимо, чтобы ребенок понял и заучил название компонентов процесса деления:

• делимое – то число, которое делят;
• делитель – то, на что делят;
• частное – конечный результат.

Далее нужно показать форму записи при делении столбиком. К примеру, нужно поделить двузначное число на однозначное:

• вначале пишется делимое – пусть это будет 98;
• справа от него рисуют уголок, как перевернутую букву «Т», в нем записывают делитель – в нашем случае 7;
• теперь определяют наименьшее число в делимом, которое делится на 7 – это 9;
• цифра 7 в числе 9 может поместиться 1 раз – значит, в частном пишем 1;
• теперь нужно умножить делитель 7 на первую цифру частного 1 – получится 7. Его надо записать под 9;
• из 9 вычесть 7 – получится 2.

Обратите внимание: полученная разность никогда не сможет быть равна или больше делителя. Если это произошло, значит, было неверно определено количество 7 в 9

• так как 2 на 7 не делится, сносят вниз следующую цифру из двузначного делимого – 8. Получили 28. Его можно поделить на 7 – получится 4;
• эту цифру нужно записать рядом с 1 – получится 14. Это и будет частным в данном примере;
• но правильно оформить решение все-таки нужно, поэтому 7 умножают на 4 – получают результат 28, который и пишут под 28. Вычитают 28 из 28 – получают 0. Его пишут под чертой, которой подводят итог решения.
• в случае если остаток не равен нулю, то это – деление с остатком.

В первый класс идет не только малыш – родители вместе с ним начинают и заканчивают школу. Учитель не всегда имеет возможность объяснить каждому ученику ту или иную тему. И вот тогда родители должны научить свое чадо, что такое умножение, деление с остатком двузначного числа на однозначное. При переходе в третий класс задание усложнится – научить нужно будет делению с остатком и трехзначного числа на двузначное. Главное, набраться терпения и не ругать ребенка из-за малейшей оплошности. Тогда все получится, и математика, возможно, станет любимым школьным предметом.

Целенаправленное запоминание

После того, как ваш ребенок освоил самые простые значения таблицы умножения, можно приступать к более сложным множителям

Тут важно использовать и элементы игры, и многие другие полезные приемы запоминания: ассоциации, повторение, дробление на части, проверочные задачки, применение на практике. Многие из примеров нужно будет заучивать, запоминать и повторять неоднократно, чтобы ваш ребенок смог потом с легкостью называть значения таблицы умножения

Лучше идти по порядку, и не пытаться выучить все сразу. Начать лучше с квадратов и умножения на 3 и 4, постепенно переходя к остальным числам.

Некоторые педагоги считают правильным способом начать изучение таблицы умножения с конца от более сложных примеров к более простым. Но лучше так не делать, чтобы избежать стресса ребенка от непонимания того, как эти значения были получены. Умножая 3 на 3, ребенок может проверить себя на пальцах, и убедиться, почему в таблице умножения стоит именно 9. А если ему сразу предложить умножить 8 на 9, и сказать, что результат нужно просто запомнить, он не сможет применить свои знания на практике, что ухудшит запоминание и может отрицательно сказаться на его мотивации.

Квадраты чисел. Квадратом числа называется его произведение на самого себя. В русской таблице умножения есть всего 10 квадратов, которые нужно запомнить. Квадраты до примера «шесть на шесть тридцать шесть» обычно запоминаются на ура, и следующие 3 квадрата обычно тоже не вызывают особых трудностей. А 10 на 10 – будет сто, что мы уже проходили ранее на предыдущих уроках.

Таблица умножения на 3. Именно на этом этапе могут возникнуть первые сложности. Если так случилось, что ребенок не может запомнить какие-то значения, то самое время начать использовать карточки. А если это не помогает, и вы знаете, что у вашего чада больше гуманитарный склад ума, то можете попробовать (о них еще будет написано ) для запоминания таблицы умножения.

Таблица умножения на 4. Здесь также можете использовать карточки и стихи. Кроме того, дайте ребенку понять, что умножение на четыре — это то же самое, что и умножение на 2 и еще раз на 2. Эти и другие простейшие арифметические закономерности, которые могут быть полезны для развития устного счета, вы найдете в данной статье.

Таблица умножения на 5. Умножение на пять обычно дается просто. Интуитивно ребенку становится понятно, что все значения этого умножения расположены через 5 друг от друга и заканчиваются либо на 5, либо на 0. Все четные числа, умноженные на 5, всегда оканчиваются на ноль, а нечетные – оканчиваются на 5.

Таблица умножения на 6, 7, 8 и 9. Есть определенная особенность изучения сложных примеров из таблицы умножения. Если ребенок выучил квадраты, а также таблицу умножения до 5, то на самом деле ему осталось выучить совсем немного, так как остальные примеры он уже знает

Это хорошо видно на этой таблице умножения, где зеленым выделены ячейки, уже освоенные ребенком к данному моменту.
В итоге, оставшиеся клетки таблицы умножения содержат всего шесть произведений, которые и являются самыми сложными, и на которые стоит обратить пристальное внимание

1. 6×7=42
2. 6×8=48
3. 6×9=54
4. 7×8=56
5. 7×9=63
6. 8×9=72

Для запоминания этих выражений таблицы умножения лучше использовать игру в карточки, чтобы довести ответы до автоматизма. Эффективнее всего использовать 12 карточек (с переменой мест множителей). Как показывает практика, у школьников, а часто и у взрослых, именно с этими шестью произведениями часто бывают некоторые проблемы.

Вот и все! Всего за несколько уроков вся таблица умножения может быть легко и быстро выучена!

Алгоритм деления в столбик

Для решения примеров делением в столбик рекомендуется пользоваться простым алгоритмом.

1. Определить в примере, где находится делимое, а где делитель.
2. Записать делимое и делитель под «уголок».
3. Определить, какая часть делимого может использоваться для первичного деления.
4. Определить сколько раз делитель умещается в выбранной части делимого.
5. Произвести умножение делителя на полученное число под уголком, результат вписать под выбранную часть делимого.
6. Найти разницу (остаток).
7. Повторить действия, пока в остатке не окажется 0.

Более подробно этот алгоритм разберем на конкретном примере.

Как научить ребенка делению в форме игры

Чтобы математика приносила ребенку удовольствие и изучалась без проблем, требуется с самого детства прививать книги любовь, а не ненависть. Поэтому обучать ей стоит в форме игры и на понятных малышу примерах.

Это могут быть способы:

• игра в магазин,
• деление конфет,
• загадки и головоломки,
• компьютерные игры,
• стишки на запоминание математических правил.

Дети охотно играют в магазин и способны освоить математические операции легко, когда стоят за воображаемым прилавком или по другую его сторону. Сейчас появились появилось много компьютерных игр, где где, чтобы попасть на следующий уровень, малышу приходится выполнять подсчёт правильно. Так как игра вовлекает, он быстро сможет научиться.

Тоже самое можно проделывать с игрушками или со временем. Если мама говорит, что что её час разделен на три части, и одну часть она может посвятить игре с ребёнком, то вместе они могут посчитать, что правильно: 60 разделить на 3. Стало 20 минут.

Пигментация и коричневые пятна

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.

2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Как научить ребенка делению 2 класс

Поскольку операция деления простых чисел является одним из важных математических действий, многие родители задумываются о том, как научить ребенка делению. Перед тем, как приступить к обучению, вы должны убедиться в том, что малыш уже умеет вычитать, складывать и умножать числа. Лучше всего приступать к изучению деления столбиком, когда ребенок отправляется в третий класс

Очень важно объяснить, что деление представляет собой процесс, по ходу которого целое разбивают на отдельные части. Не забудьте учесть знания таблицы умножения – убедитесь в том, что кроха уверенно знает ее

Перед тем, как серьезно приступить к обучению, попробуйте освоить эту нехитрую науку в игровой форме. Для того чтобы сформировать у малыша представление о том, что деление – это разбор целого на части, дайте ему несколько предметов и попросите разделить между членами семьи или игрушками. При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.

Потренируйтесь на кубиках. Возьмите парное количество этих элементов и предложите ребенку разделить их поровну между собой и вами. Варьируйте задание. Добавьте такое количество кубиков, чтобы их общее количество делилось на три или шесть. Затем можно усложнить задачу и делить на восемь, семь или девять. После выполнения каждого задания тщательно анализируйте результат вместе с малышом. Он должен понимать сам процесс. Если что-то ему непонятно, постарайтесь доходчиво это объяснить. Не зацикливайтесь на определенных предметах. Постоянно меняйте их, чтобы ребенок приспосабливался делить любые объекты.

Важно! Для начала составляйте задания таким образом, чтобы малыш проводил действия с четным количеством объектов. Таким образом, у ребенка получится одинаковое количество предметов

Это пригодится на следующем этапе, чтобы дать понять малышу, что деление – операция обратная умножению.

Вместе с этим ищут и читают:

Методы обучения

Теперь вам необходимо решить, как научить ребенка делить. Если он уже перешел в третий класс, трудностей у вас возникнуть не должно. Для начала объясните малышу зависимость между делением и умножением. Продемонстрируйте ему, как правильно делить столбиком, используя таблицу умножения. Рассмотрим следующий пример: 3*4=12. Расскажите ребенку, что три и четыре – это множители, а двенадцать – произведение. Проиллюстрируйте ему это на наглядном примере. Покажите ему, что если двенадцать разделить столбиком на три, получится четыре.

Объясните ученику, который перешел в третий класс, что категории, описывающие деление, называются «делимое», «делитель», «частное». Продемонстрируйте это наглядно с помощью таблицы. Рассмотрите как можно больше примеров, чтобы малышу было понятнее. Это пригодится в дальнейшем, когда вы будете осваивать деление столбиком. По сути, вам необходимо научить кроху смотреть на таблицу умножения «наоборот».

Перед началом занятий еще раз вспомните категории деления. Теперь попробуем объяснить все наглядно. Например, разделим число девятьсот тридцать восемь на семь. Запишем числа, чтобы делить их столбиком. Если вы только начинаете обучение, то ребенку, который пошел в третий класс, будет проще для начала делить числа без остатка. Теперь показываем ученику числа делимого и предлагаем ему выбрать наименьшее число, которое будет больше, чем делитель. Выбираем число девять. Теперь предложите малышу ответить, сколько чисел семь может содержаться в числе девять? Правильный ответ – одно. Поэтому записываем единичку.

Умножаем семь на один, получаем семь. Этот результат мы записываем под девяткой из числа девятьсот тридцать восемь. Вычитаем от девятки семерку в столбик. В остатке получаем два. Аналогичным образом записываем результат. Полученное число меньше, чем делитель. Таким образом, нам необходимо его увеличить. Объединяем его со следующим неиспользованным числом – тройкой. «Плюсуем» тройку и двойку. Продолжаем процесс деления согласно с алгоритмом. В итоге мы получаем число – сто тридцать четыре.

Самое главное в процессе обучения малыша, который перешел в третий класс, чтобы он усвоил простой алгоритм. Развивайте наблюдательность у крохи, проводите аналогии с другими математическими действиями, больше играйте и наблюдайте за природой.

Раскладываем число на компоненты

Работа с однозначными числами достаточно проста. Нужно выучить таблицу умножения и просто совершать действия в обратном порядке. Потребуется немного практики, чтобы научиться решать подробные примеры на скорость и в уме. Это будет полезно особенно при написании математических диктантов, когда учитель диктует задание, а детям нужно только записать правильный ответ.

Сложности наступают в тот момент, когда приходится решать примеры с теми числами, которые за пределами таблицы. Например:

Делимое — 90, делитель — 5. Нужно найти частное.

Ребенку сложно в уме выполнить требующиеся операции, поэтому нужно предложить ему разделить большое число на составляющие:

90 = 40+50;

40:5 + 50:5 = 8+10=18; значит 90:5=18.

Если ученик в первом классе хорошо усвоил состав числа, то у него не возникнет сложностей и с похожими операциями: 72 — это 60+12, 84 — это 60+24, 93 — это 30+30+30+3.

Деление на трехзначное число

Деление на трехзначное число

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

• Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
• Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
• Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
• Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
• Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
• Запишите 2864 под 2864, получается в разности 0. Ответ 204

Как выучить деление и умножение с ребенком

Самый элементарный метод, с помощью которого можно научиться умножать и делить, представлен наглядной демонстрацией разделения предметов на равные части или же увеличения этих долей. В роли предметов, которые используются в качестве обучающего реквизита, должны выступать предметы, вызывающие в уме школьника интерес.

Умножение и деление однозначных чисел

Для деления однозначных чисел на однозначные лучше всего использовать таблицу умножения, но перед этим следует объяснить своему чаду, что деление – это действие, противоположное умножению. Сделать это можно с помощью любого правильного деления натуральных чисел, к примеру, 2 умножить на 4 будет 8. Придерживаясь данного примера, показать карапузу делительный процесс:

• разделить 8 на любой множитель, например, на число 2;
• в ответе получится 4, то есть множитель, который не был использован при делении.

Таким методом также делятся многозначные (двухзначные) числа на однозначные. А для того, чтобы освоить процесс умножения однозначных чисел, вместе с малышом достаточно лишь постепенно учить таблицу умножения.

Алгоритм деления однозначных чисел

Умножение и деление двузначных чисел

В целях разъяснения дошкольнику процесса умножения двухзначных цифр опытные педагоги рекомендуют прибегать к итальянскому методу или методу «решетки». Для начала следует на листе бумаги начертить мини-таблицу два на два: одно число записать по длине, а другое – по ширине таблицы. Каждую клетку нужно разделить по диагонали ровной линией, после чего в образовавшиеся треугольники вписать результат умножения чисел (отдельно десятки, отдельно единицы).

Далее вместе с ребенком сложить «произведения» строго по диагонали, результат подписать. Произведение будет равно значению, которое образуется в процессе чтения цифр снизу вверх и направо.

Некоторые родители предпочитают использовать китайско-японский способ умножения в процессе обучения своих детей. Он может показаться более сложным, чем метод «решетки», но на деле все не так страшно. Следует всего лишь нарисовать цифры линиями, посчитать «узлы», которые образовались при пересечении, и «собрать» из них произведение. В процессе подсчета учитываются следующие моменты:

• количество узлов, которые получились при пересечении линий, обозначающих десятки перемножаемых чисел = количество сотне произведения;
• узлы, получившиеся при пересечении прямых, обозначающих единицы и десятки умножаемых цифр = количество десятков произведения.

Обратите внимание! Что касается количества узлов, образовавшихся путем пересечения линий, которые обозначают единицы умножаемых чисел, то оно равняется количеству единиц произведения. Если ребенок еще не проходил метод деления двухзначных цифр «столбиком», то нужно объяснить ему на более простом языке

Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:

Если ребенок еще не проходил метод деления двухзначных цифр «столбиком», то нужно объяснить ему на более простом языке. Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:

64 = 30 + 30 + 6.

Малышу сразу все станет понятно: 30 и 6 мы сможем поделить на 3, после чего нужно будет только сложить результаты, т. е. 66 / 3 = 10 (получили в процессе деления 30 на 3) + 10 (30 поделили на 3) + 2 (6 поделили на 3).

66 / 3 = 22. Здесь не был использован метод разделения в столбик, но карапуз сразу поймет ход рассуждений и выполнит простые вычисления без труда.

Как научить ребенка делить?

Существуют некоторые достаточно тривиальные подходы, которые используются почти всеми родителями чтобы научить ребенка делить:

1.

Речь идет о методе деления каких-либо конкретных объектов между людьми. То есть, вам достаточно только предложить вашему ребенку разделить между вами какие-либо конфеты или яблоки, и он сможет сделать это легко. Теперь только останется объяснить ему, что таким образом он поделил некоторое количество на два и научить его записывать действие цифрами. Объяснить вы сможете, задавая ему логические вопросы. Для начала пусть он ответит на вопрос о том, сколько было конфет с самого начала. Потом задайте ему вопрос о том, сколько было человек. В результате вы получите одну большую цифру и одну поменьше. Получается, что деление необходимо производить из большого числа с помощью маленького.

Чтобы закрепить и понять, как научить ребенка делить по-настоящему, вы должны предложить ему произвести деление различного количества предметов между несколькими людьми.

2.

Действенные методы того, как ребенка научить делению, можно почерпнуть из занимательной арифметики Энгельмана, где в интерактивной и понятной форме излагаются элементарные действия. В частности, учитывая то, что деление по программе проходят после умножения, Энгельман предлагает объяснять его, как умножение наоборот. Для примера можно нарисовать восемь кубиков по два в столбик и объяснить ребенку, что если восемь разделить на два, то получится четыре, то есть по четыре кубика в каждом столбике или колонке. А вот если восемь разделить на четыре, то получится по два кубика в каждом ряду.

3.

Целесообразно также будет подключить более практические навыки чтобы научить ребенка делить. Например, взять десять вишен и попросить ребенка поделить их между вами поровну. Он может начать деление по одной, откладывая по очереди вам и себе по вишенке. Затем получившиеся кучки можно будет посчитать и убедиться, что он действительно поделил правильно и десять вишен между двумя участниками дадут каждому по пять ягодок. После того, как он освоит сам механизм деления на осязаемых предметах, вы можете переходить к абстрактным понятиям.

Также полезно будет разъяснить ребенку обратную связь между умножением и делением. Не забывайте постоянно проверять знания ребенка, пока деление простых чисел не будет проходить автоматически.

«Новые» правила деления слов на слоги в русском языке (Московская школа. Литневская Е. И. Русский язык: Краткий теоретический курс для школьников. М., 2006)

Слогораздел по «новым» правилам проходит в месте наибольшего спада звучности. В любом НЕначальном слоге звучность нарастает от начала слога к его вершине. Самые звучные — это гласные, затем идут по порядку сонорные, звонкие и шумные согласные. Последний слог может быть закрытым, то есть звучность в нем нарастает и спадает.

1. В слове столько слогов, сколько гласных; два гласных не могут находиться в пределах одного слога.

Слог — это один звук или несколько звуков, произносимых одним выдыхательным толчком воздуха: во-да, на-у-ка.  Согласные звуки являются неслоговыми. При произношении слова согласные звуки «тянутся» к гласным, образуя вместе с гласными слог.

2. Слог может состоять из одного звука (и тогда это обязательно гласный) или нескольких звуков (в этом случае в слоге, кроме гласного, есть согласный или группа согласных): ободок — о-бо-док; страна — стра-на; ночник — но-чник; миниатюра — ми-ни-а-тю-ра. 

3. Слоги бывают открытыми и закрытыми.

• Открытый слог оканчивается на гласный звук: во-да, стра-на.• Закрытый слог оканчивается на согласный звук: сон, лай-нер.• Открытых слогов в русском языке больше. Закрытые слоги обычно наблюдаются в конце слова: но-чник (первый слог открытый, второй — закрытый), о-бо-док (первые два слога открытые, третий — закрытый).• В середине слова слог, как правило, оканчивается на гласный звук, а согласный или группа согласных, стоящих после гласного, обычно отходят к последующему слогу: но-чник, ди-ктор.• В середине слова закрытые слоги могут образовывать непарные звонкие согласные , , , , , , , , (сонорные): май-ка, Сонь-ка, со-лом-ка.

4. Иногда в слове могут писаться два согласных, а звучать один, например: изжить . Поэтому в данном случае выделяются два слога: и-зжить. Деление на части из-жить соответствует правилам переноса слова, а не делению на слоги.

То же самое можно проследить на примере глагола уезжать, в котором сочетание согласных зж звучит как один звук ; поэтому деление на слоги будет — у-е-зжать, а деление слова для переноса — уез-жать.

Особенно часто ошибки наблюдаются при выделении слогов у форм глаголов, оканчивающихся на -тся, -ться. Деление вить-ся, жмёт-ся является делением на части для переноса, а не делением на слоги, поскольку в таких формах сочетание букв тс, тьс звучит как один звук . При делении на слоги сочетания букв тс, тьс целиком отходят к последующему слогу: ви-ться, жмё-тся.

5. При сочетании нескольких согласных в середине слова:

• два одинаковых согласных обязательно отходят к последующему слогу: о-ттечь, да-нный;

• два и более согласных обычно отходят к последующему слогу: ша-пка, ра-вный. Исключение составляют сочетания согласных, в которых первым является непарный звонкий (сонорный): буквы р, рь, л, ль, м, мь, н, нь: мар-ка, зорь-ка, бул-ка, стель-ка, дам-ка, бан-ка, бань-ка. То есть если после сонорного согласного следует парный по глухости / звонкости согласный, граница слогов проходит между ними. Пример: Спар-так. 

• если после й следует любой другой согласный, граница слогов проходит между ними: лай-ка, лай-нер. Дело в том, что й по звучности считается близкой к гласным.

Как объяснить деление дошкольнику

Малыши-дошколята вовлекаются в процесс деления с самого раннего возраста, например, когда угощают конфетами друзей, делятся игрушками в песочнице. Поэтому задача родителей заключается в том, чтобы обобщить этот детский опыт для освоения азов арифметики, дать понимание принципа деления, то есть разделения предметов на равные доли. При этом базовыми знаниями, необходимыми для освоения деления в дошкольном возрасте, является понимание, что такое целое, больше/меньше. Если с этими понятиями ребёнок знаком, то можно вооружаться играми и на их основе поэтапно объяснять деление.

Делим поровну

Для начала нужно показать малышу на доступном для его понимания уровне, что такое деление, используя наглядность. В этом поможет игра Тебе и мне поровну.

Инструкция:

1. Малыш получает 6 конфет.
2. Взрослый просит поделить конфеты на двоих так, чтобы у каждого было одинаковое количество.
3. Ребёнок раскладывает конфеты по одной, пересчитывая их в обеих кучках.
4. После того, как конфеты поделены, юный математик ещё раз пересчитывает их в каждой кучке, а затем считает, сколько сладостей всего.
5. Количество делителей можно увеличивать, но делимое всегда должно делиться без остатка. Так у ребёнка формируется представление о том, что такое поровну.

Деление с остатком

Освоив деление без остатка, можно переходить к следующему этапу игре Всем поровну и хвостик.

Инструкция:

1. Ребёнок получает 4 яблока.
2. Взрослый просит разделить их поровну между тремя членами семьи.
3. Оставшееся яблоко является остатком, который получается тогда, когда поровну поделить нельзя.

Разобравшись с делением поровну и с остатком, можно переходить к освоению абстрактного деления, то есть вычислениям с использованием цифр, а не конфет-яблок-игрушек. Для этого нужно сказать, что первое число это то, что мы делим: конфеты, игрушки, яблоки, а второе участники этого деления, то есть члены семьи, друзья. Но главное здесь, сколько предметов в итоге будет у участников.